The Bar Model
A representation used to expose mathematical structure
The bar model is used in teaching for mastery to help children to 'see' mathematical structure. It is not a method for solving problems, but a way of revealing the mathematical structure within a problem and gaining insight and clarity to help solve it. It supports the transformation of real-life problems into a mathematical form and can bridge the gap between concrete mathematical experiences and abstract representations. It should be preceded by and used in conjunction with a variety of representations, both concrete and pictorial, all of which contribute to children’s developing number sense. It can be used to represent problems involving the four operations, ratio and proportion. It is also useful for representing unknowns in a problem and as such can be a precursor to more symbolic algebra.
It is helpful to introduce children to the bar model as part of a sequence of learning so they can connect their understanding of the real world to this mathematical representation. In the NCETM Primary Professional Development Materials they are introduced in Year 1. The bar model can continue being used to expose mathematical structure throughout school maths and beyond. The NCETM Secondary Professional Development Materials contain a section on bar models for use in Key Stage 3 and beyond.
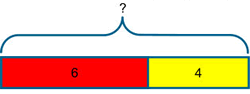
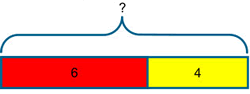
The bar model supports understanding of the relationship between addition and subtraction in that both can be seen within the one representation and viewed as different ways of looking at the same relationships.

This diagram encapsulates all of the following relationships;
a = b + c ; a = c + b ; a – b = c ; a – c = b
To prepare young children for the bar model it is a good idea to encourage them to line up objects in a linear arrangement when representing addition and subtraction problems.
Such arrangements will also help children to organise their counting. The physical objects can then be replaced, in time, with linking cubes and with a bar drawn next to it. The question can then be asked “what’s the same, what’s different?” to support the children in their reasoning and in making sense of the bar as an abstract representation of the physical objects. It is useful for children to work in pairs with one manipulating the cubes, while the other records by drawing the bars and then writing the number sentence underneath. The children can then swap roles.
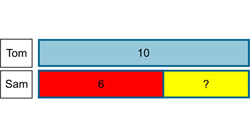
Sam had 10 red marbles and 12 blue marbles. How many marbles did he have altogether?
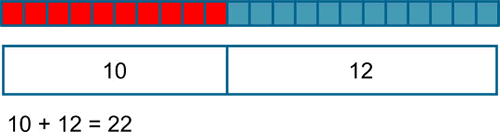
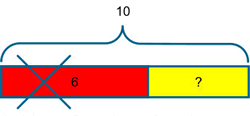
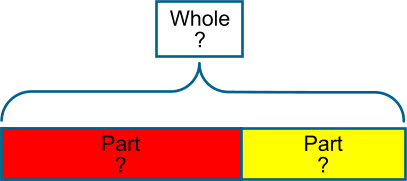
In problems involving addition and subtraction there are three possible unknowns as illustrated below and given the value of two of them the third can be found.
The examples below illustrate a variety of ways that the bar might be used for addition and subtraction problems. A question mark is used to indicate the part that is unknown.
Addition
|
Addition
|
Subtraction
|
Subtraction
|
Equivalence
The model can be rearranged to demonstrate equivalence in a traditional layout
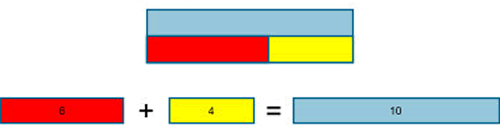
Pupils need to develop fluency in using this structure to represent addition and subtraction problems in a variety of contexts using the bar model. The model will help children to see that different problems share the same mathematical structure and can be visualised in the same way. Asking children to write their own problems, using the bar as the structure will help to consolidate this understanding.
All of these concepts involve proportional and multiplicative relationships and the bar model is particularly valuable for representing these types of problems and for making the connections between these concepts visible and accessible.
Multiplication
Notice how each section of the bars in the problem below has a value of 4 and not 1. This many-to-one correspondence, or unitising is important and occurs early, for example in the context of money, where one coin has a value of 2p for example. It is also a useful principle in the modelling of ratio problems.
Peter has 4 books
Harry has five times as many books as Peter.
How many books has Harry?

4 × 5 = 20
Harry has 20 books
Division
When using the bar model for division it is the image of sharing rather than grouping which is highlighted in this representation.
Mr Smith had a piece of wood that measured 36 cm.
He cut it into 6 equal pieces.
How long was each piece?
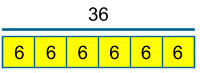
36 ÷ 6 = 6
Each piece is 6 cm
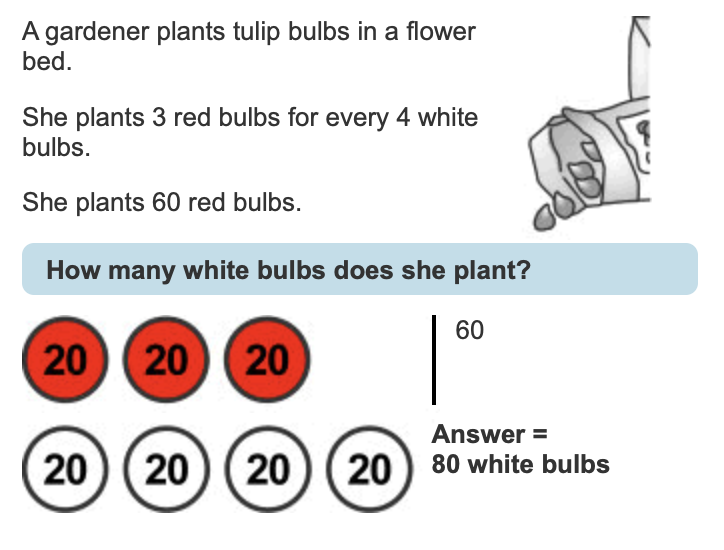
Problems Involving Proportion
When modelling problems involving proportion it is useful to divide the bar into equal parts so that the proportional relationship and multiplicative structure are exposed.
Once the value of one part is labelled, the other parts can be identified as they are the same, for example in this KS2 SATS Question.

Fractions
The bar model is valuable for all sorts of problems involving fractions. An initial step would be for pupils to appreciate the bar as a whole divided into equal pieces. The number of equal pieces that the bar is divided into is defined by the denominator. To represent thirds, I divide the bar into three equal pieces, to represent fifths I divide the bar into five equal pieces. A regular routine where pupils are required to find a fraction of a number by drawing and dividing a bar, using squared paper would be a valuable activity to embed both the procedure and the concept and develop fluency.
Find 1/5 of 30
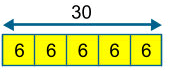
The same image can be used to find 2/5 or 3/5 of 30 etc.
Finding the original cost of an item that has been reduced in a sale is one that pupils find particularly tricky. The ease at which such problems can be solved is demonstrated below:
A computer game is £24 in the sale. This is one quarter off its original price. How much did it cost before the sale?

The bar represents the original cost. It is divided into quarters to show the reduced cost of £24.
£24 ÷ 3 = £8, giving the value of three sections of the bar. The final section of the bar must also be £8, since it represents the same proportion as each of the other sections.
£8 × 4 = £32
The original cost of the computer game is £32
Percentages
Problems involving percentages are solved in a similar way to those involving fractions. The key is to divide the whole into equal parts.
A computer game is reduced in a sale by 30%. Its reduced price is £77. How much was the original price?
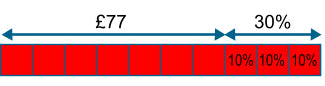
Dividing the bar into ten equal pieces allows us to represent 30% and keep the other pieces the same size.
£77 ÷ 7 = £11
The original cost (the whole bar) is £11 × 10 = £110
Problems involving Ratio
The ratio problem outlined below is represented with double sided counters. These can be used as an alternative representation to drawing a bar. The advantage of this is that they can be moved around to represent a change in relationship.
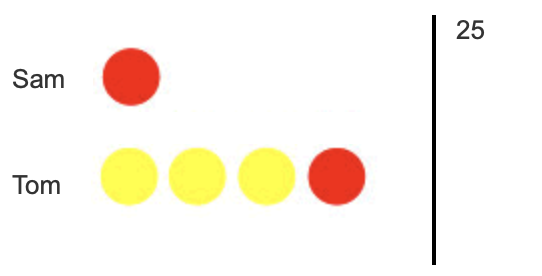
Sam and Tom have football stickers in the ratio of 2 to 3. Altogether they have 25 stickers. If Sam gives half of his stickers to Tom, how many will Tom have?
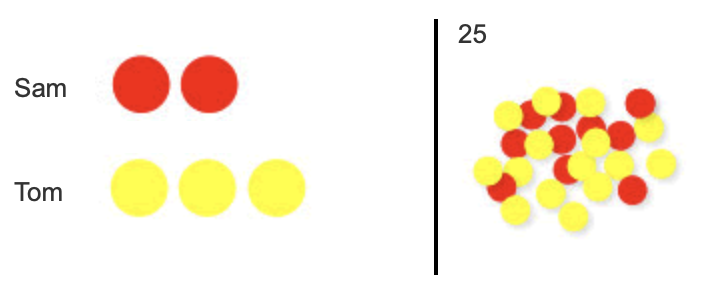
Step 1
Represent the ratio
Step 2
Recognise that if together the counters have a value of 25 then one has a value of 5
Step 3
Give half of Sam's stickers to Tom
Step 4
Multiply 5 by 4 to give the total value of Tom's stickers
Answer:
5 × 4 = 20

Notice how the many-to-one correspondence, as discussed above, allows this problem to be modelled efficiently. Children may at first use a one-to-one correspondence (i.e. each counter having a value of 1) and represent the problem using 25 counters, setting them out in a two to three ratio as illustrated below.

Children can then be supported in transferring their understanding to many-to-one correspondence as illustrated above (i.e. that every 5 counters in each column can be replaced with one counter worth 5). The flexibility of appreciating that the value of one counter can change depending on the context and the total quantity helps to develop the pupils’ algebraic reasoning.
Notice how the strategy explored above supports this KS2 SATS question