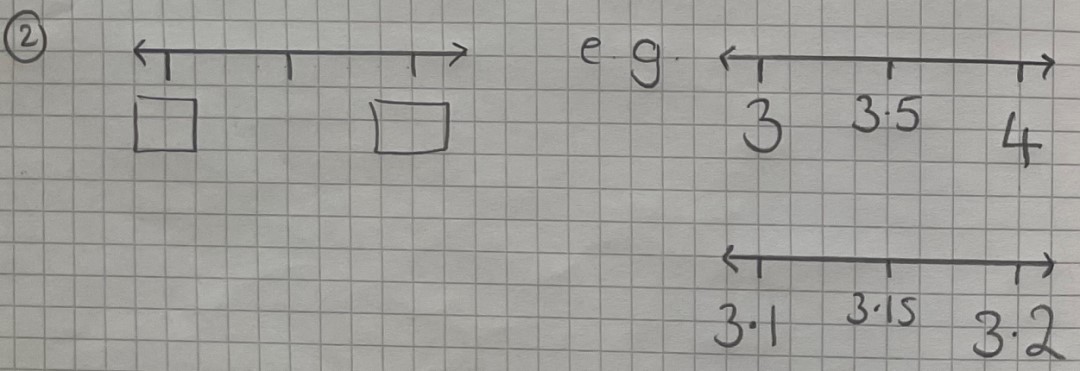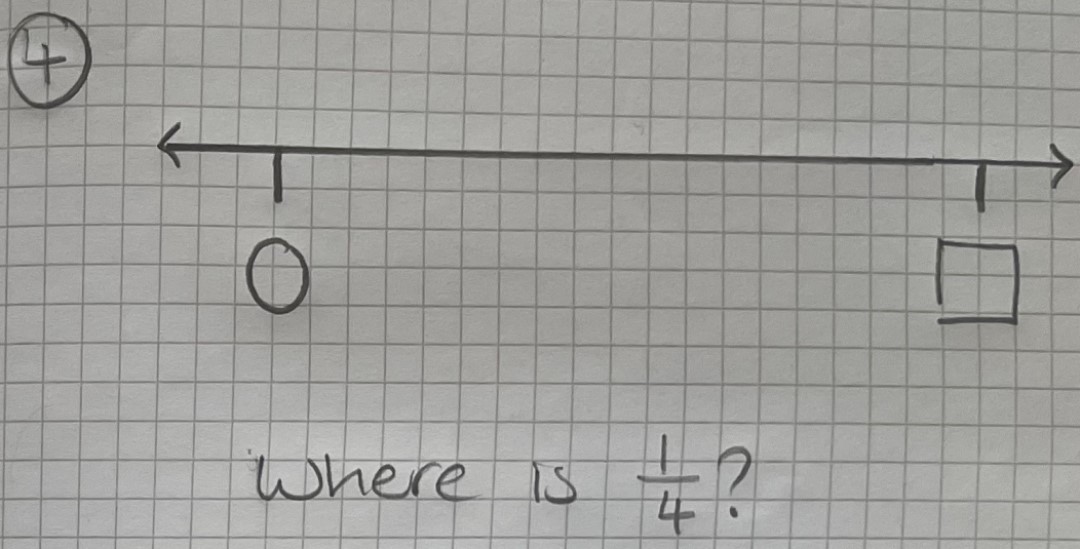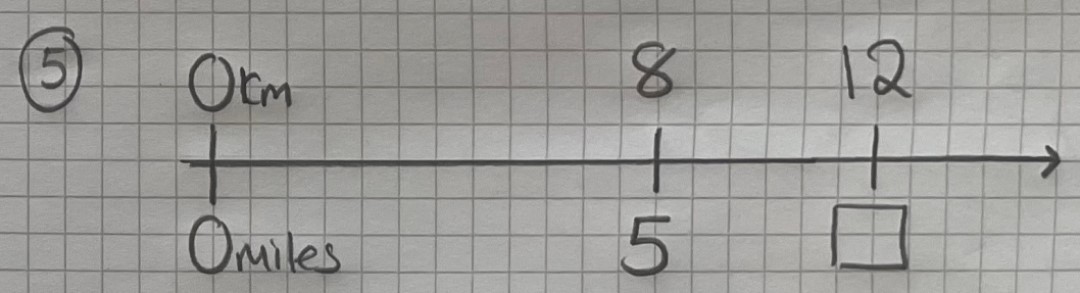Five ways to use number lines in secondary maths

If you’ve yet to harness the power of the number line in your secondary maths classroom, we’d like to share some ways you can use this simple but versatile representation with your students. In this feature, we focus on a podcast episode with the NCETM’s Assistant Director for Secondary, Becky Donaldson, which explored ways of using number lines in secondary maths.

1. Explore different aspects of the linear number system

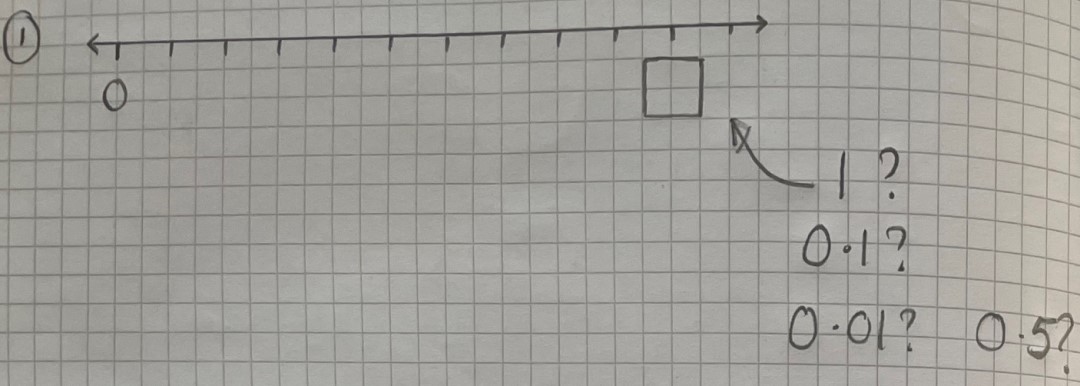
Our first number line offers a simple way to zoom into different parts of the linear number system to probe and develop students’ understanding. It’s a straight line with a zero on the left-hand side, ten intervals marked on the line and an empty box on the tenth interval. Arrows at each end of the line indicate the infinite nature of the linear number system, both above and below zero. 

We might start by placing the number 1 in the box, to assess understanding from KS2. Can students place the relevant tenths on the number line? Will they use fractions or decimals? This may be an opportunity to assess whether they are confident with both forms of the number. 

We can repeat the exercise by placing 0.01 in the box, and then 0.001, which may expose some misconceptions. Would finding the midpoint first help? An interesting way to deepen students’ understanding still further would be to place 0.5 in the box. Would students be able to reason that, this time, we will have a tenth on every other interval and between them 5 hundredths, 15 hundredths and so on? Comparing completed number lines can enable students to start to make connections, see patterns and continue to develop that number sense.

2. Understand rounding with a blank number line

Children may come into secondary school knowing the conventions of rounding — perhaps with some kind of memory aid to help them decide what to do when the relevant digit is below 5, or equal to/above 5 — but have no context for this. This next number line allows us to explore what that rounding process actually looks like. It is a straight line, with arrows to show infinity, and three intervals marked, one at either side and one at the midpoint. 

We will place a pair of numbers, for example 3 and 4, in the two boxes and then ask students to identify the midpoint. Once they know 3.5 is the midpoint, can they identify where 3.2 would round to? Our number line provides a visual aid to understand the concept of rounding, why and when we round up and down, as well as demonstrating the importance of the midpoint. It can be repeated with a range of numbers, including decimals, so students can practise rounding to various degrees of accuracy, including moving them on to the language of decimal places and significant figures. 

3. Use number lines to explore bounds

Finding bounds can be a tricky topic for Year 10 and 11, but the number line representation can be a useful, visual way to approach it. Rounding is a foundational concept for bounds, but there is often an extensive gap between rounding at the start of KS3 and tackling bounds later in KS4. Using the number line representation when exploring bounds for the first time, perhaps recapping rounding using the same representation first, can provide a clear conceptual link between rounding and bounds. 

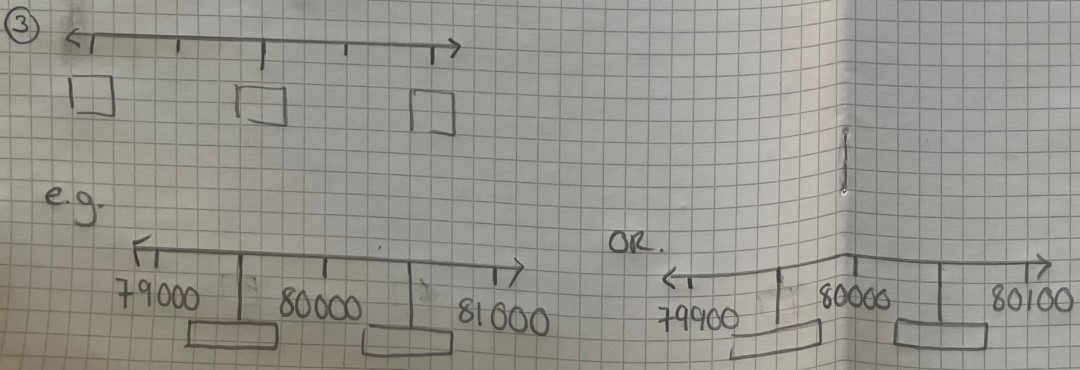
Here we start with another blank number line, with an empty box at either end of the line and an empty box at the midpoint. Two more intervals are marked at the midpoints between each box. We can start with a simple question: if a tank has a capacity of 80,000 litres to the nearest thousand litres, what is the maximum and minimum capacity of the tank? 

We place 80,000 – our capacity – at the midpoint and then ask the students to think about what quantities they can place in the boxes on either side. Encourage them to notice that we are working in litres, and to think about the litres either side of 80,000. They should then place 79,000 in the left-hand box and 81,000 in the right-hand box. Now students have the midpoints between each of those thousands to consider: 79,500 and 80,500. 

You can ask students to think about the values within this range and how they know they will round to 80,000, as well as what the values outside of this range will round to. Use their rounding knowledge to talk about how the upper bound is actually 80,499.9…, and why we still use 80,500 rather than 80,499.9… in calculations involving the upper bound. This leads nicely into expressing the lower and upper bounds using the inequality 79,500 ≤ x < 80,500. 

A useful bit of variation might be to use the same numbers but instead round to the nearest 100 or 10,000, so that students can really develop a good understanding of finding the different lower and upper bounds through that exploration of the midpoints. A further, important, piece of variation is to change the values from continuous to discrete. How would your original question and bounds be different if we were talking about the capacity of a sports stadium rather than a tank?

4. Use a number line to explore fractions as a value

Many teachers will agree that fractions can be a tricky topic. One of the reasons for this is that they exist as both a proportion and a value. Our next number line is a great starter activity, which can be used regularly, building over time, to enable the exploration of fractions as a value. It also gives students the opportunity to reason and develop mathematical thinking.

The concept is very simple. We start with a straight line, with arrows to show infinity, a zero at one end and an empty box at the other. Into this empty box we place a range of different numbers, asking students to estimate where ¼, as a value, would be on the line. 

So, into our box we might place 1, asking students to estimate where on the line the ¼ would be marked. Now, we might change the number in the box to 2. Do the students realise that they need to move their ¼ so it’s now halfway between its former position and zero? What if the number in the box is 5 or 10?

We can then employ variation to further deepen students’ understanding, by changing the number in the box to a fraction. Can they reason where ¼ would be if ⅓ is placed in the box? If ⅕ is placed in the box, do they know that ¼ would now move to the right of the box?

Once students are familiar with the premise, how would they respond if ⅛ was placed in the box? Could they reason that their line would need to extend beyond the box, and that ¼ should be placed the exact same distance along the line again because ¼ is equivalent to ²⁄₈? This idea is developed in Checkpoint 2 from the Arithmetic procedures including fractions deck of the NCETM’s Checkpoints slides.

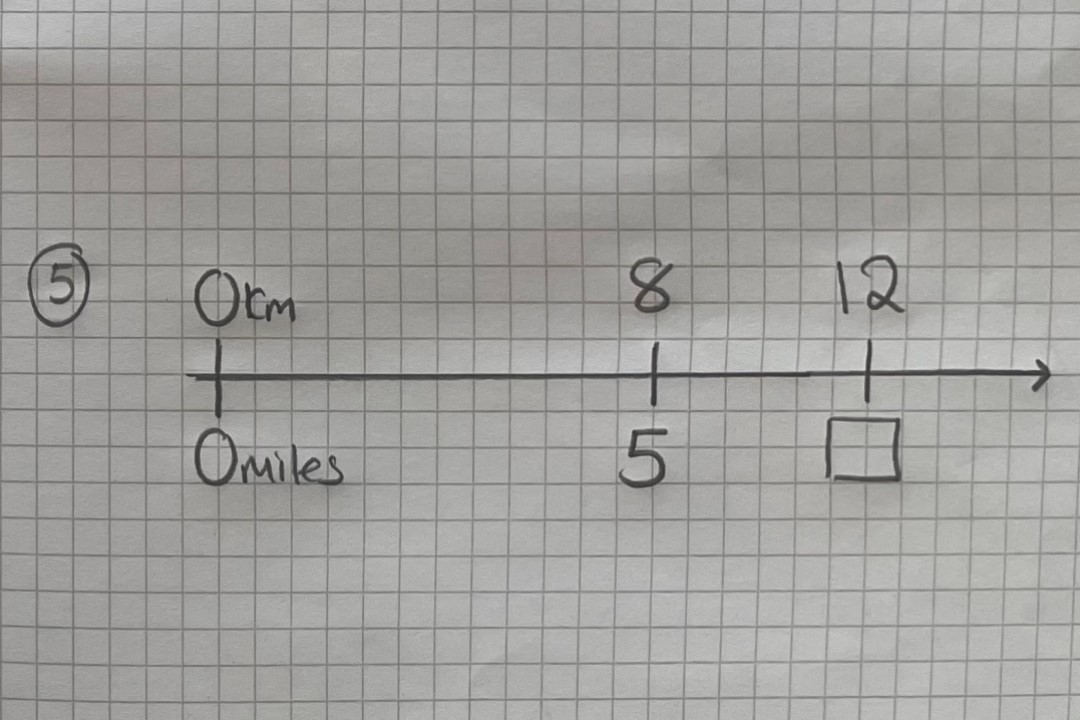
5. Use double number lines to explore relative quantities

There are a whole host of different ways to use double number lines, but their use as a visual way to explore the relationship between different units of measure is particularly effective. In this example, we use a number line to reveal the multiplicative structures between miles and kilometres, but the same approach can be used to compare euros and pounds, lbs and kgs, or even problems such as ‘if eight chocolate bars cost £5, how much would twelve bars cost?’. 

Our number line is a simple line, with an arrow to indicate infinity, and kilometres marked above the line and miles beneath. We start at zero, and mark 8km and 12km at intervals on the top. 5 is placed under 8 and an empty box is placed under 12. 

Students may rush to suggest what number would go in the box. However, with this activity we are slowing the students down and asking them to look closely at the relationships between the values and the multiplicative structures; we are asking them to explore other things that they know. 

So, our first question might ask the students to consider, if you know 8 and 5 are related, what else do you know? They may focus on the left part of the line, identifying that half 8 is 4, so 4 will be equal to 2.5. Or they may work on the right-hand side and double 8 to make 16 and 5 to make 10. They may then be able to work out what number should go into the box. 

Using the number line representation in this way allows us to give students ownership of exploring the relationships between numbers. Rather than just giving them a unitising method, we are exposing the underlying structure of those multiplicative relationships. Students have an opportunity to reason and discuss the maths, and are able to work towards a deeper conceptual understanding.