How one secondary school is using Checkpoints at KS3

Have you tried our Year 7 Checkpoints diagnostic activities in your classroom or department yet? How have you been using them? Are you finding the teacher notes help you or your colleagues to learn what students might have covered in primary school and how? We have begun collecting stories to find out how schools are using Checkpoints and inspire teachers to think creatively about how they will work best with their students.

Mandy Sharples is Head of Maths at Up Holland High School near Wigan in Lancashire. A Secondary Mastery Specialist (with NW3 Maths Hub), she began introducing a Teaching for Mastery approach with Year 7 in September 2020. In September 2021, she started to supplement her scheme of work with NCETM Checkpoints as they began to be published.

We visited Up Holland school in May 2022 to see how her department were getting on and how the Year 7s were finding the Checkpoints.

Up Holland’s Year 7s are organised in two halves of the year group, with three sets in each. There is a fourth ‘nurture group’ across the year, taught by a single teacher for maths, English and some other subjects to smooth the transition from primary school. All groups follow a common scheme of work and teachers of Year 7 maths meet weekly in a common non-contact period to discuss progress and plan.

Below are some examples of the Checkpoints we saw used in lessons, and how teachers were using them. Click/tap slides to enlarge.

Comparing lengths: used as prior assessment with set 2

Students worked in pairs on their whiteboards to find the conversions. A class discussion followed, looking at the relevant conversion in each case, with useful discussions over the prefixes ‘kilo’ and ‘cent’. The teacher was able to reflect her observations back to the class:

“What this has made me realise is that you are finding it difficult to remember conversion facts, but that you find switching between units relatively straightforward if you have the relevant fact”.

Extra challenge is suggested in the support slide for this Checkpoint – asking students about the greatest and smallest possible values in each inequality – which might be the next step for these students.

Mandy has identified from question level analysis (QLA) in KS4 that unit conversions is a weakness in GCSE performance at Up Holland, so this is something she is keen to work on with teachers and students in KS3. Understanding the learning sequence, right from primary school and through KS3, that is required to successfully answer questions at GCSE is important when using QLA. The teacher notes and support slides to the Checkpoints clearly lay out the primary school learning and what is expected in KS3.

Decimal differences: used as prior assessment with set 3

For many students, the starting point of this Checkpoint was difficult to access and needed scaffolding by the teacher, who was using it as prior assessment for a topic due to be taught a fortnight later. Students found it difficult to perceive the constraints imposed by working with a two-digit integer as minuend, with a single digit (and a bit) to be subtracted to produce the given difference. It seemed that students lacked a mental picture to support subtracting whole numbers and ‘bits’, suggesting that use of manipulatives might be helpful to support them to build mental representations of decimal numbers.

Interesting insights began to emerge from students that started to access the problems. Many made the classic mistake of subtracting one too many in the first equation, omitting to include the sum of the tenths - for example, 10 – 4.8 = 6.2

The teacher said that what he learned from this episode would inform his thinking about teaching the topic later, mentioning that he often consulted with a primary teacher about how a topic might have been addressed in primary school.

He might choose to represent the problems on a number line or to use place value grids, as suggested in the support slide for this Checkpoint. Or he might use one of the Additional Activity slides that has the same problems but laid out in a way that suggests a column subtraction approach and supports correct use of place value:

Checkpoints are designed to enable teachers to diagnostically assess prior knowledge and understanding brought from primary school by Year 7s. However, any teacher in possession of a resource they value will want to use it wherever they perceive it is most applicable to the needs of their students. So we were interested to see where else Checkpoints are being used at Up Holland to assess understanding.

Comparing place value in decimals: used as retrieval practice with
set 1

The Up Holland scheme of work is designed so that retrieval practice is spaced throughout, and teachers have begun using Checkpoints to support this. By listening carefully to student responses and using probing questions suggested on the support slides, teachers are able to ascertain depth of understanding.

For this activity, students worked in pairs on mini-whiteboards, discussing their solutions as they went, while the teacher circulated, picking up any issues she identified.

Following paired work, the teacher asked individual students to explain each answer to the class. Most students used the strategy of writing the words as fractions and then converting to decimals to compare - for example, 31 tenths = 31/10 = 3.1

Question f) provided further challenge with some addition required.

Students marked their answers and the teacher asked, “Did anyone get 6 out of 6?” – to which roughly half the class put up their hands. The teacher will now be able to use this response, along with what she diagnosed while circulating, to plan any further learning or consolidation that students will need to do on this topic.

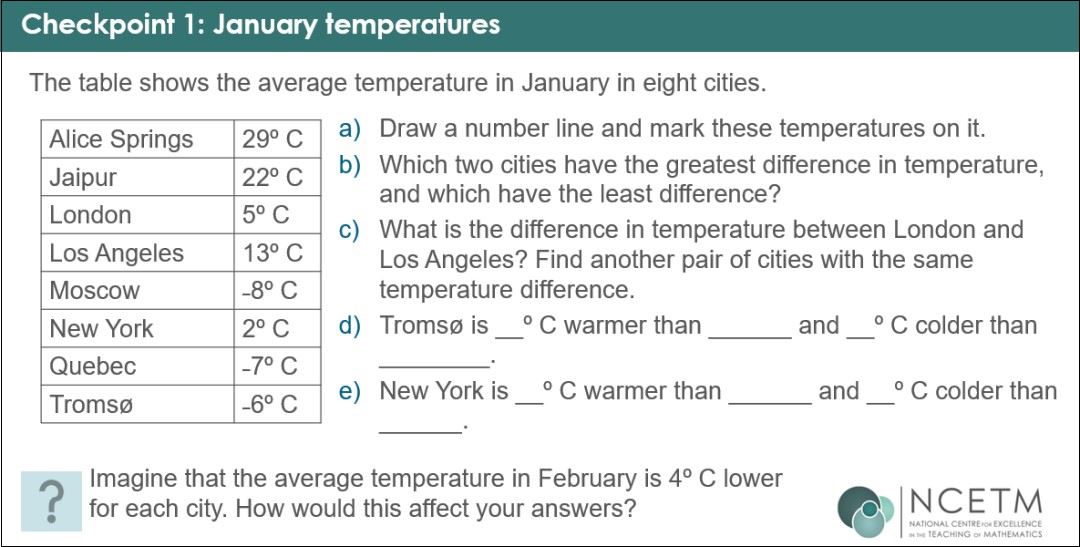
January temperatures: used as prior assessment

We asked Mandy if she has a favourite Checkpoint, and she told us she’d enjoyed using ‘January temperatures’.

She found this Checkpoint useful in assessing that her students struggled to draw a number line, particularly understanding the importance of equally spacing the numbers.

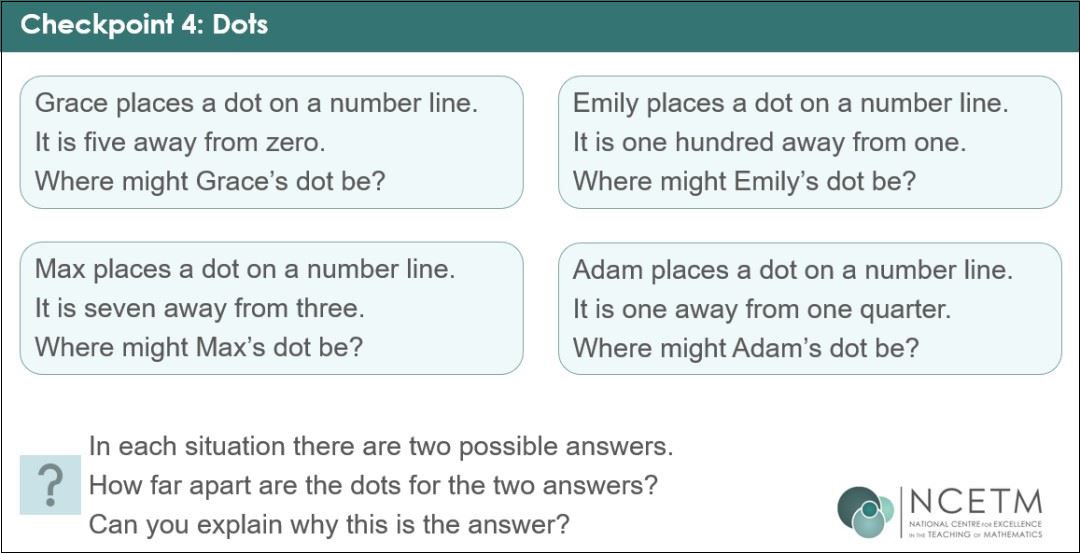
Following her use of this Checkpoint, she plans to use ‘Dots’ to assess understanding of the symmetry of negative and positive numbers.

Find our full set of Checkpoints activities.

Join a Maths Hub ‘Years 5-8 Continuity’ Work Group for professional development on maths across the primary-secondary transition, using Checkpoints resources.

And if you are already using Checkpoints – please get in touch. We are actively looking for more schools to share their experiences.