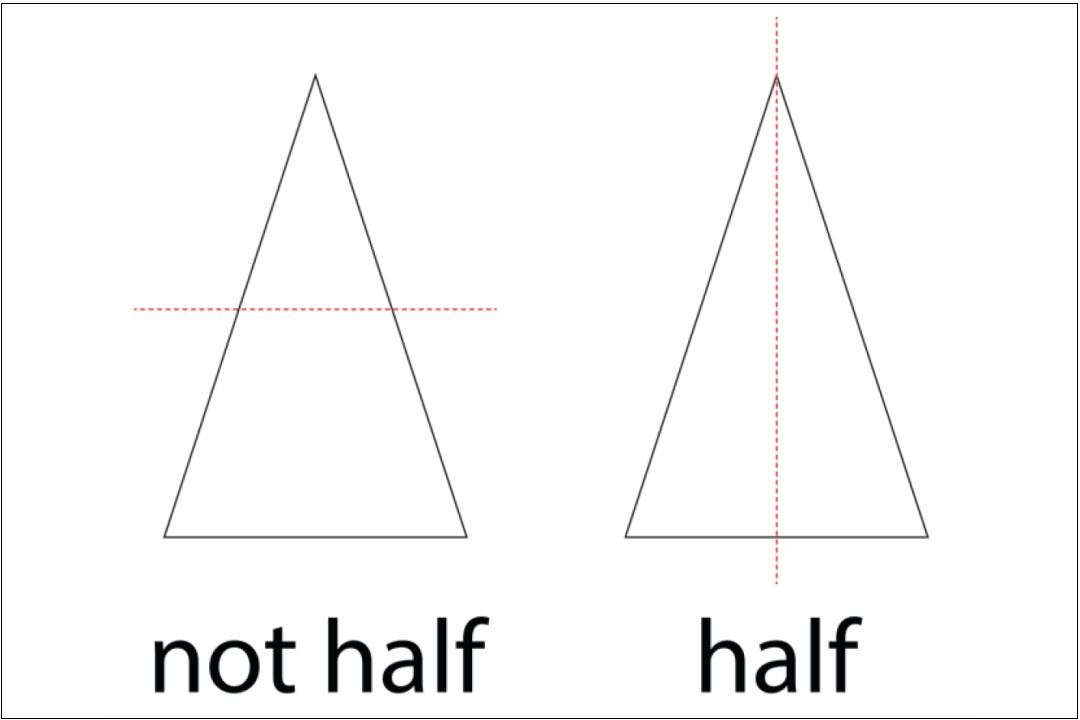Learning fractions shouldn’t be difficult

Do your pupils find it difficult to understand fractions? This article describes how a well-sequenced curriculum that builds conceptual understanding, in small, supported steps, can help fractions to make sense.

When the NCETM first set up links with schools in Shanghai, teachers from England asked the Chinese teachers about the complexity of teaching fractions. Chinese teachers were confused by the question – they didn’t perceive fractions as difficult to teach, or to understand. What we observed in Shanghai is that learning of fractions doesn’t begin until children start to learn about multiplicative relationships. Furthermore, the learning is carefully sequenced to build on prior learning, in small steps. The different ways of understanding fractions are worked on explicitly:

• to describe the size of each equal part relative to the whole
• as operators (a symbol indicating an operation to be performed - for example, '¾ of 20' uses ¾ as an operator)
• as numbers, each of which has a place in the linear number system
• to describe a proportional relationship.

What was learned from Shanghai is now reflected in the sequence of learning suggested in the NCETM Curriculum Prioritisation resource.

The resource, based on the classroom slides and pedagogical support offered by the Primary Mastery Professional Development Materials, offers a coherent journey through fractions, as well as the rest of the primary maths curriculum. The sequencing is designed to build a secure understanding of fractions, how they are written, what each part of that notation represents, and the different uses of a fraction.

Very little sight of fractions in Key Stage 1

How you introduce fractions and connect learning is important, as children’s understanding of number in KS1 is around developing confidence and mental fluency with whole numbers, counting, and place value.

So, fractions are not really learned about in any depth in KS1. They are just looked at briefly towards the end of Year 2, in Unit 10 of the Curriculum Prioritisation resource.

Children will have learnt about the numbers 0 and 1 and be aware that sometimes we have more than zero but less than one. They will have heard fractions being used in everyday contexts such as ‘half an hour’. These familiar understandings will now be given more concrete mathematical meanings. Children are encouraged to recognise familiar fractions such as ½, understanding that it is one of two equal parts of an object, shape or quantity.

Carefully sequenced progression and depth in Key Stage 2

In KS2, fractions form a significant part of the curriculum.

Year 3

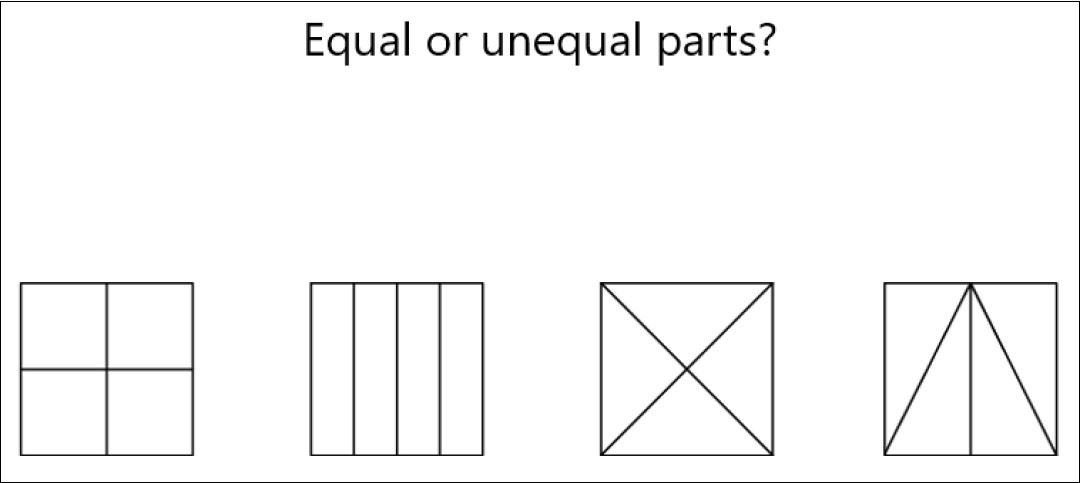
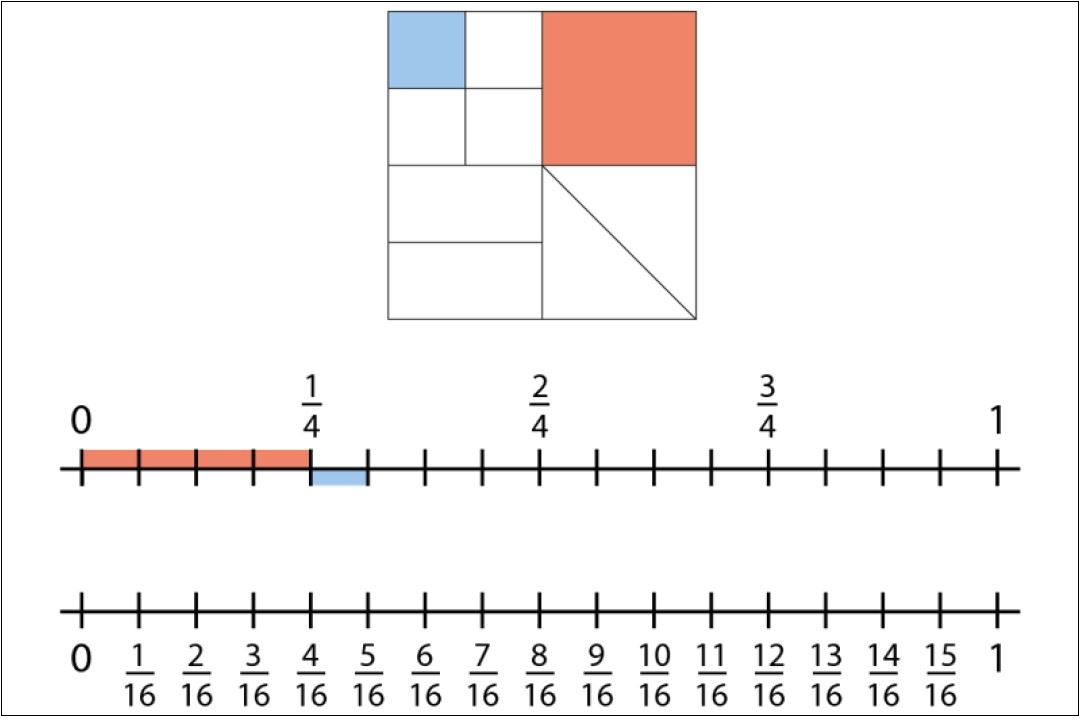
In Year 3, pupils begin by understanding how a fraction can be used to describe the size of each part relative to the whole, when a whole has been divided into equal parts.

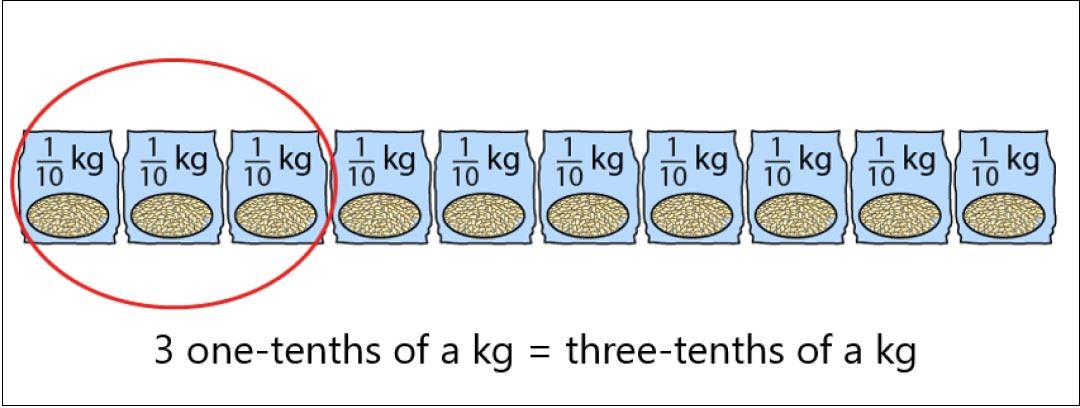
Time is spent working with unit fractions (those with the numerator 1) before moving on to non-unit fractions, first by building up from adding unit fractions. These are the foundation for all future fraction concepts.

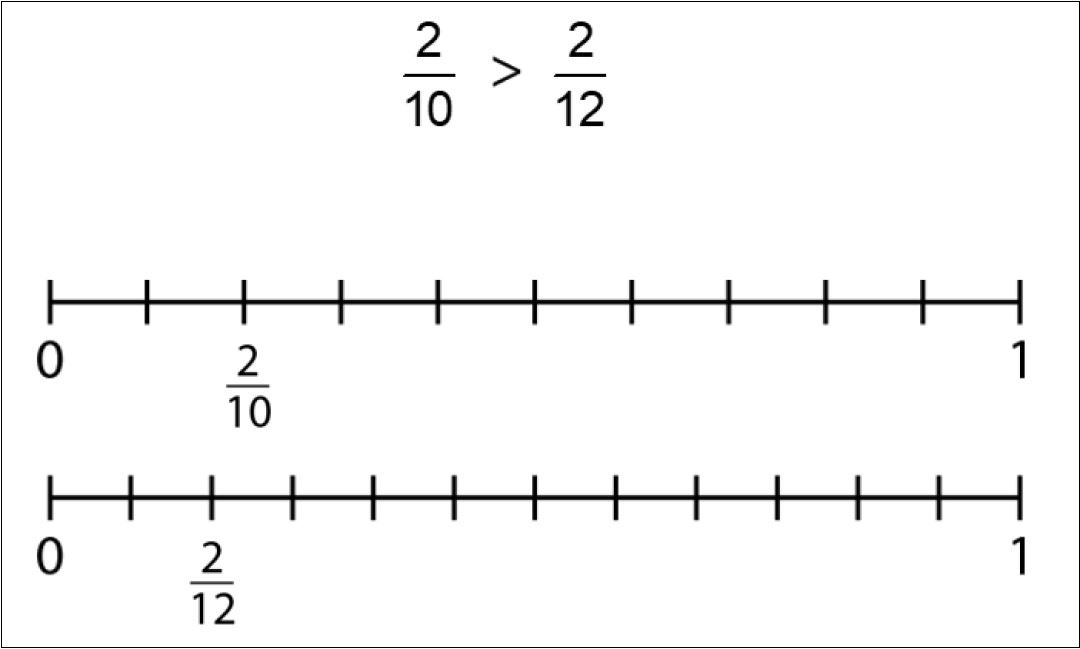
Children can also compare the size of fractions that have either the same numerator, or the same denominator.

In Year 3, pupils also:

• reason about the location of any fraction within 1 in the linear number system
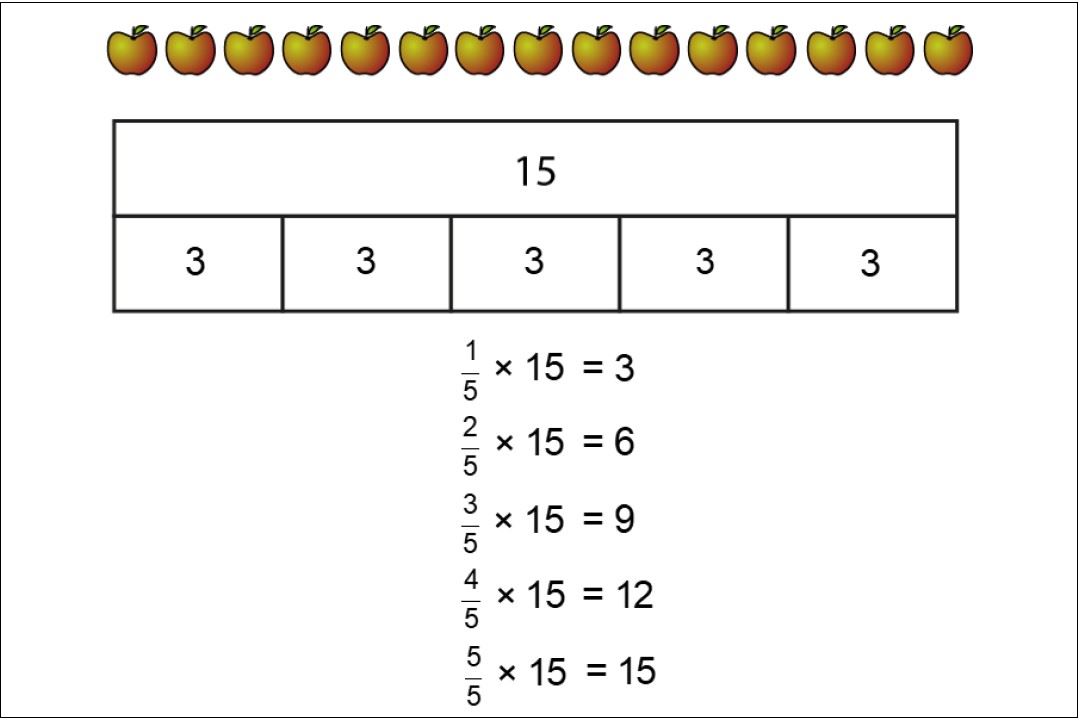
• use known division facts to find unit fractions of quantities
• add and subtract fractions with the same denominator.

Year 4

In Year 4, after thoroughly reviewing Year 3 work, pupils move on to look at fractions greater than 1– both as mixed numbers and improper fractions – understanding what they represent and how to convert between the two. In Year 3, they learned about a fraction (less than 1) representing a number in its own right, and how to locate this in the linear number system (by placing on a number line ). Without careful attention, this is a mathematical understanding that children can often miss, thinking only of a fraction as part of a whole. In Year 4, this understanding is now extended to include fractions greater than 1, allowing pupils to add and subtract fractions across 1.

Year 5

Year 5 children begin to find non-unit fractions of quantities, building on fluency with multiplication and division facts and their understanding of how to find unit fractions of quantities developed in Years 3 and 4.

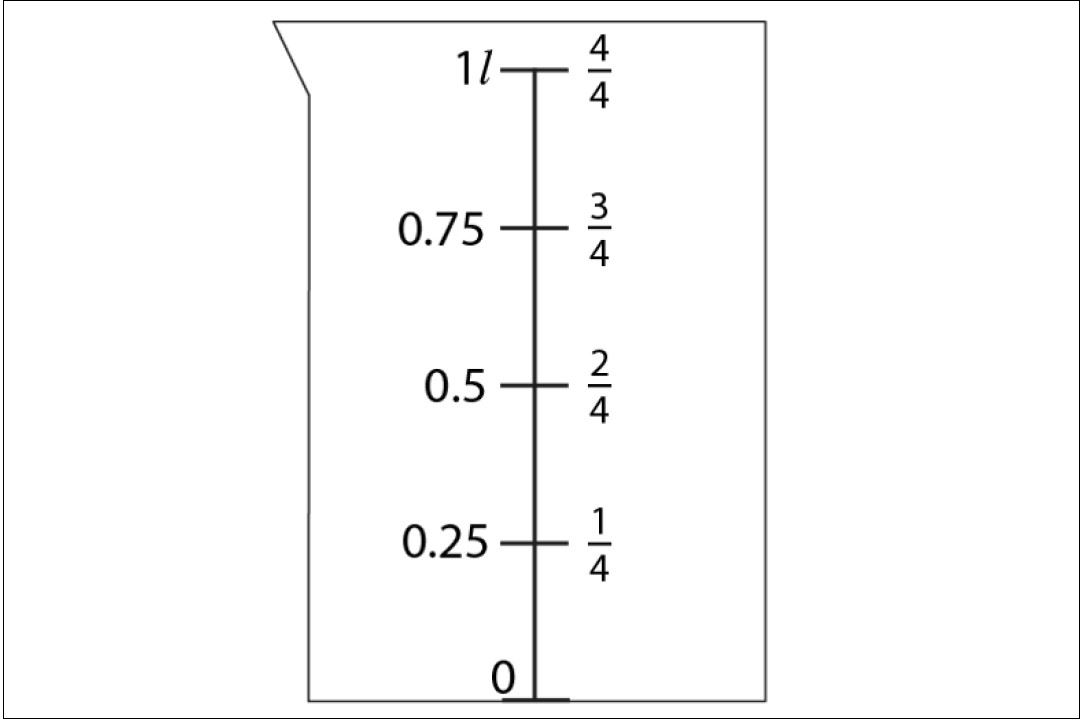
They also explore equivalent fractions and simple fraction/decimal equivalents, knowing that they can be used to represent the same value.

This knowledge is extended beyond the 0 to 1 interval, knowing for example that 3.2km and 3⅕km are two different ways of writing the same distance.

Year 6

Throughout learning about fractions, each new step builds upon and reinforces prior knowledge and understanding. In Year 6, for example, when pupils simplify a fraction, they know, thanks to earlier work, that it does not change its value, and the simplified fraction has the same position in the linear number system as the original fraction.

Pupils use this to understand common denominators and be able to use them to compare and add/subtract fractions.

So, we hope that's given you an idea of how careful sequencing of lessons on fractions across five school years can reduce the risk of pupils leaving primary school with shaky understanding. And we hope it's tempted you to look further into our Curriculum Prioritisation materials. Our two-minute video will give you an introductory tour of the materials.