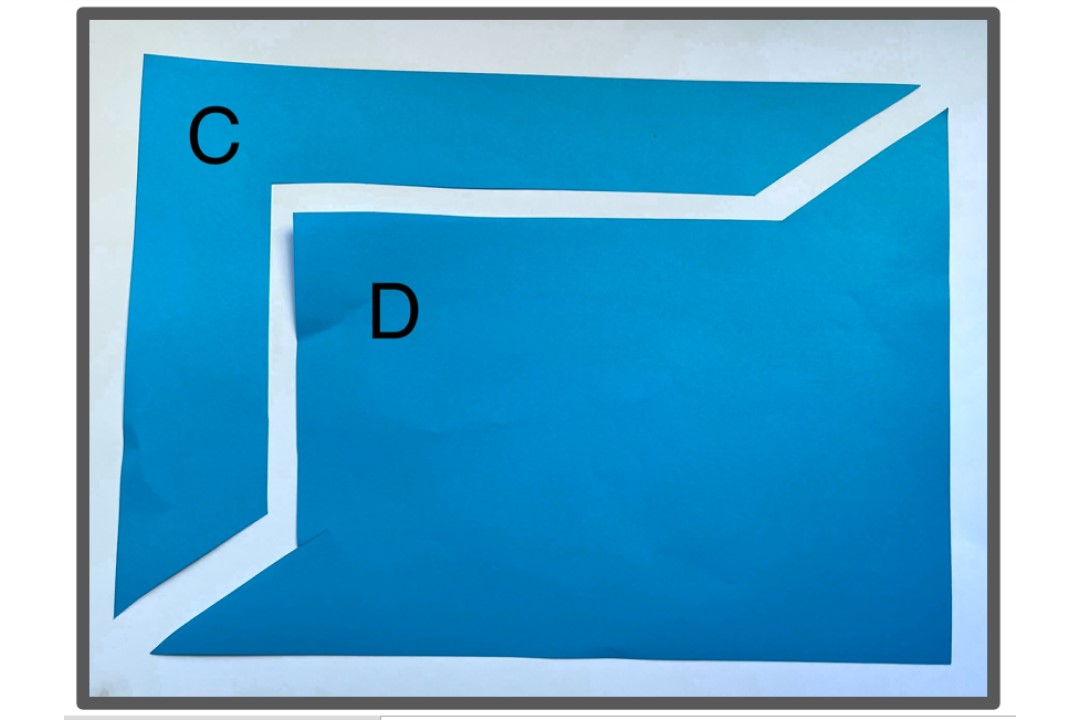
How often have you marvelled at students’ tendency to confuse perimeter with area? Have you noticed them scrabbling to remember formulae and whether to add or multiply side lengths, without using an understanding of the concepts?

The NCETM Checkpoints Perimeter and area deck uses a series of short activities to allow you to diagnose what your Year 7s understand from primary school - both conceptually, and in terms of being able to use the formulae flexibly in familiar and unfamiliar situations.

Slides are shown here for illustration and do not display the animations embedded in the PowerPoint itself. You can download the full Perimeter and area slide deck from our Checkpoints page.

The deck contains the slides shown below, as well as suggestions for how you might use them, pedagogical guidance, suggested questioning and information about how the topic should have been covered at primary school. There are also some additional activities, useful for when you feel that something needs to be explored in greater depth.

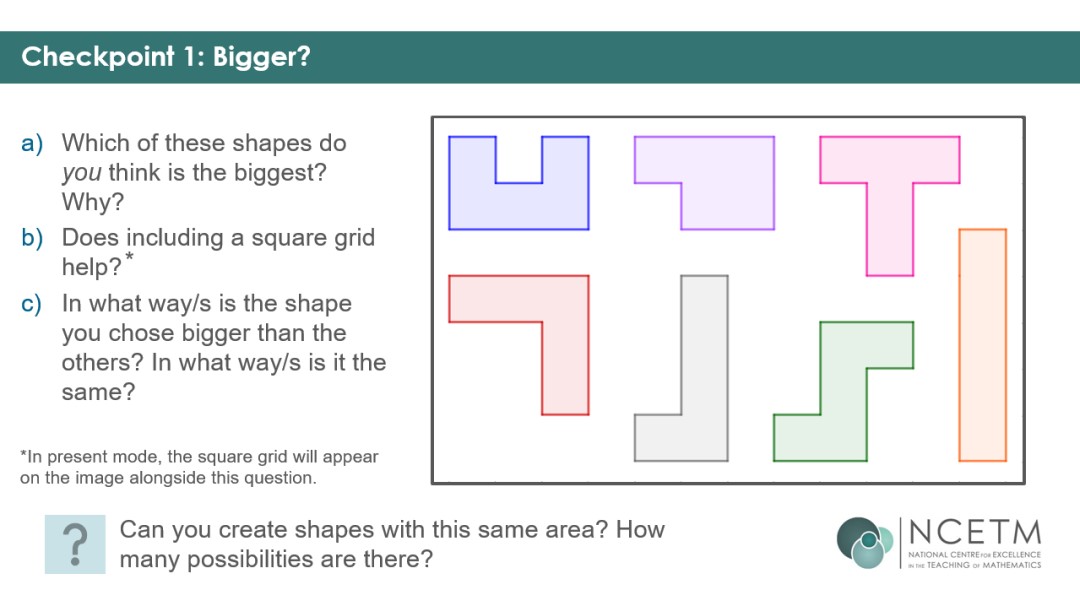
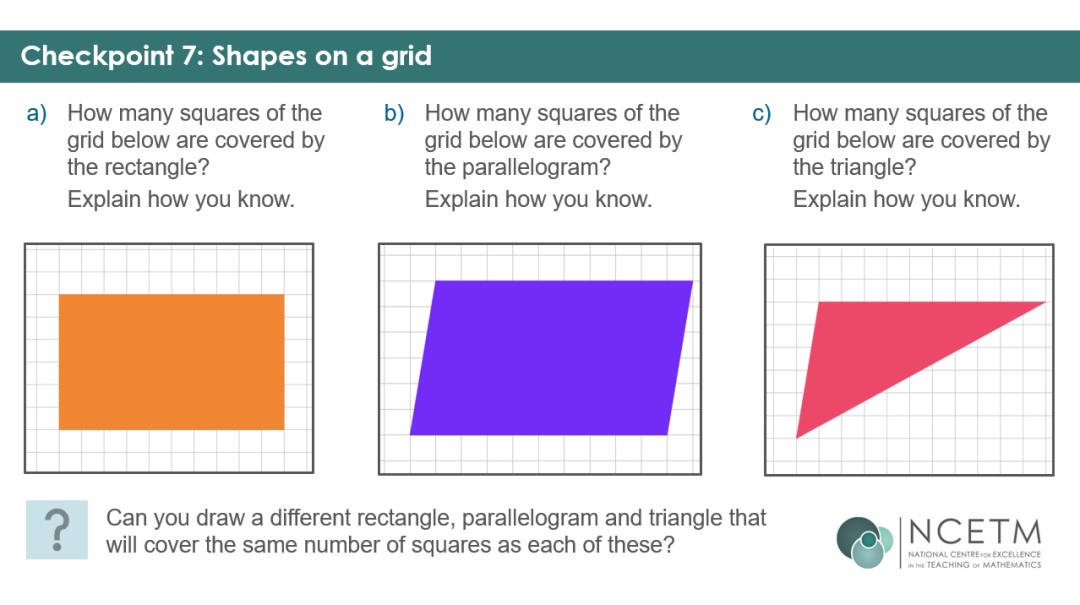
The deck begins with a look at which shape is ‘bigger’ – the vagueness of the term designed to draw out more precise terminology students might know. As part b animates, a grid appears, overlaying the shapes, which may incline students to say they are the ‘same’ size, and prompt discussion about ways they could be considered ‘different’ sizes.

The second Checkpoint focuses purely on the concept of perimeter, encouraging students to reason about the relative length of sides, without any numbers to distract. Like the previous activity, discussion and argument are key to understanding where students are at, as well as allowing them to develop their mathematical oracy.

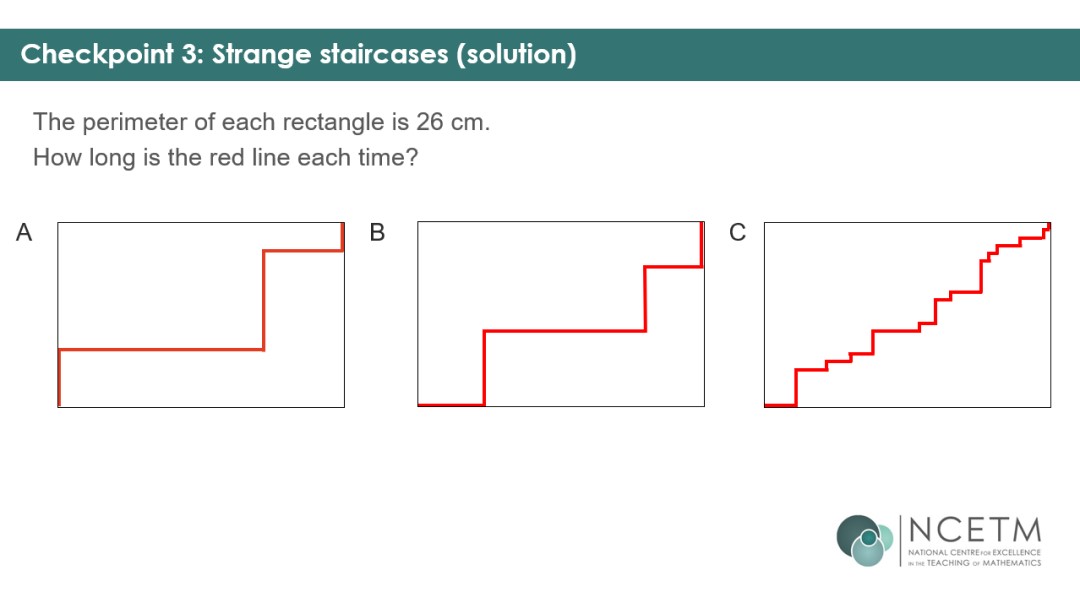
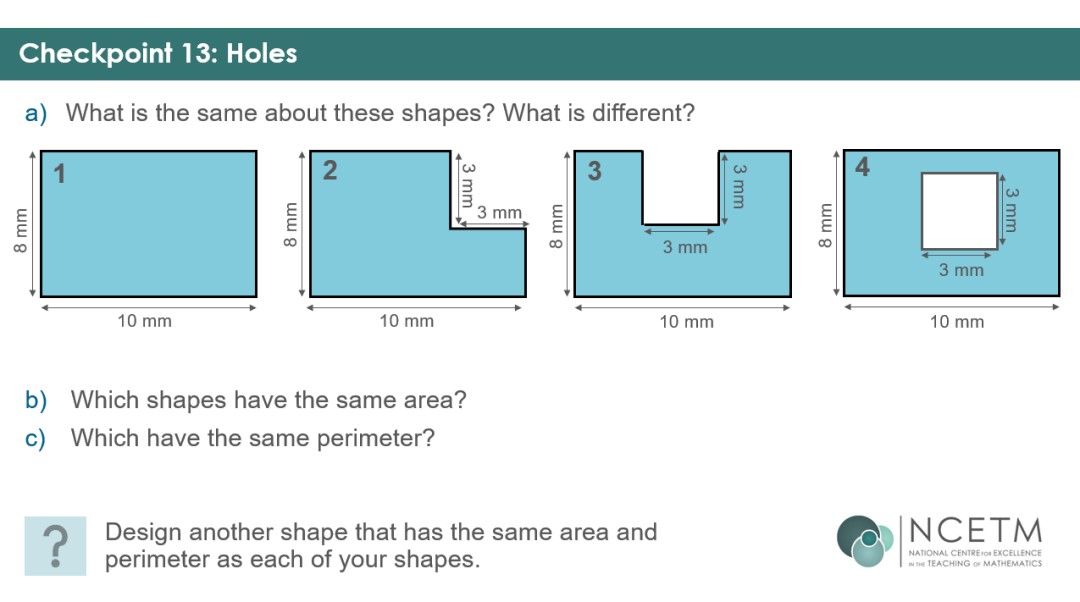
Checkpoint 3 allows you to check students’ ability to reason about equal lengths in rectilinear shapes – a key awareness for finding missing lengths when working with compound shapes in KS3.

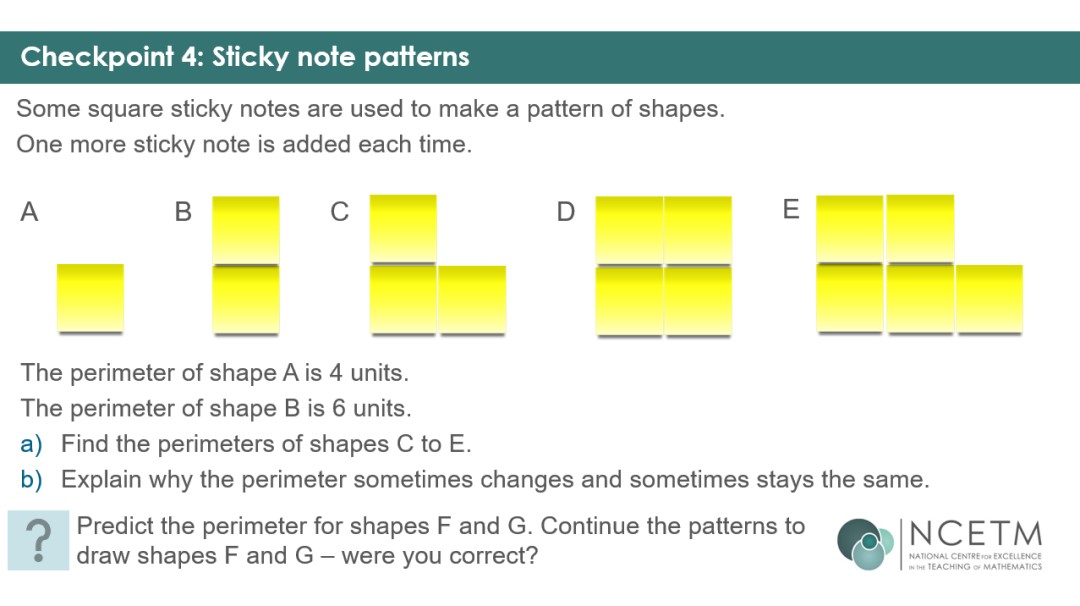
Do your Year 7s make the common mistake that greater area means greater perimeter? Checkpoint 4 should expose and challenge this misconception. Can they identify which sides cease to be on the perimeter when a new sticky note is added?

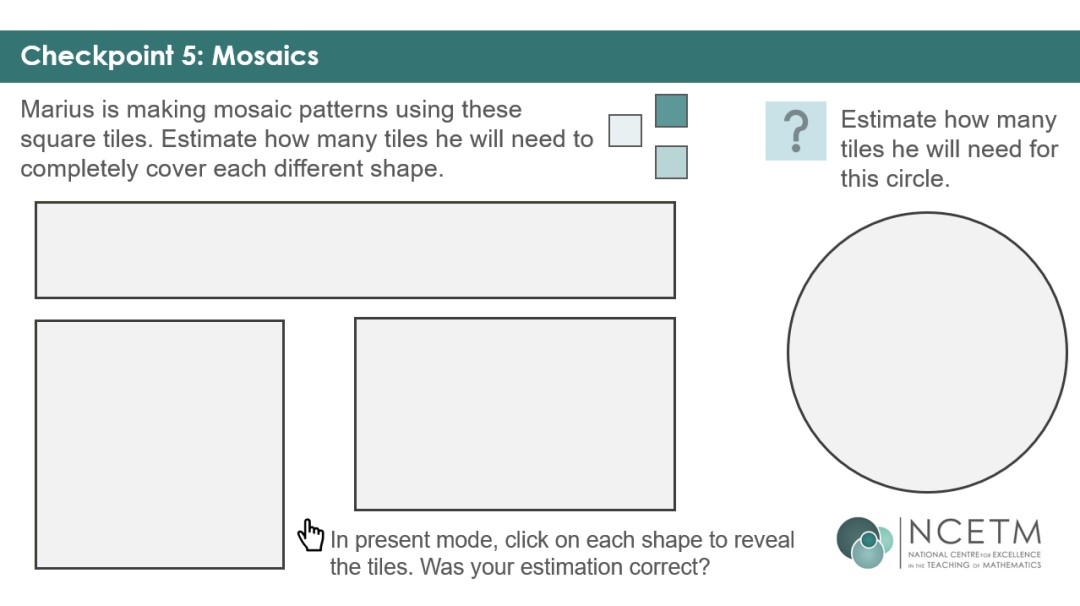
Checkpoint 5 moves on to area, but still focusing on the concept rather than calculation. This allows you to observe spatial reasoning skills and to assess understanding of concepts. Clicking on each shape overlays the tiles needed to fill each shape, but there are too many to sensibly count. This allows you to assess estimation skills and efficient methods for finding rectangular areas.

Checkpoint 6 is the first one that deals with area and perimeter simultaneously, so that you can check that students don’t confuse the two concepts, and to check for the common misconception, that a change in one necessarily means a change in the other. Students should be encouraged to describe and explain the changes spatially rather than by calculation. For example, “When I remove the red square, the area is less but the perimeter remains the same because the two edges in the perimeter that are removed are replaced by a yellow edge and a purple edge”, rather than “When I remove the red tile, the area becomes 8 and the perimeter is still 12”.

When the Checkpoints move on to calculation, the emphasis is still on deep conceptual understanding, encouraging students to be clear about how formulae are derived – or indeed to derive them themselves – rather than on trying to remember and apply. Listen to students reason about the areas of the shapes – what does this expose about their understanding?

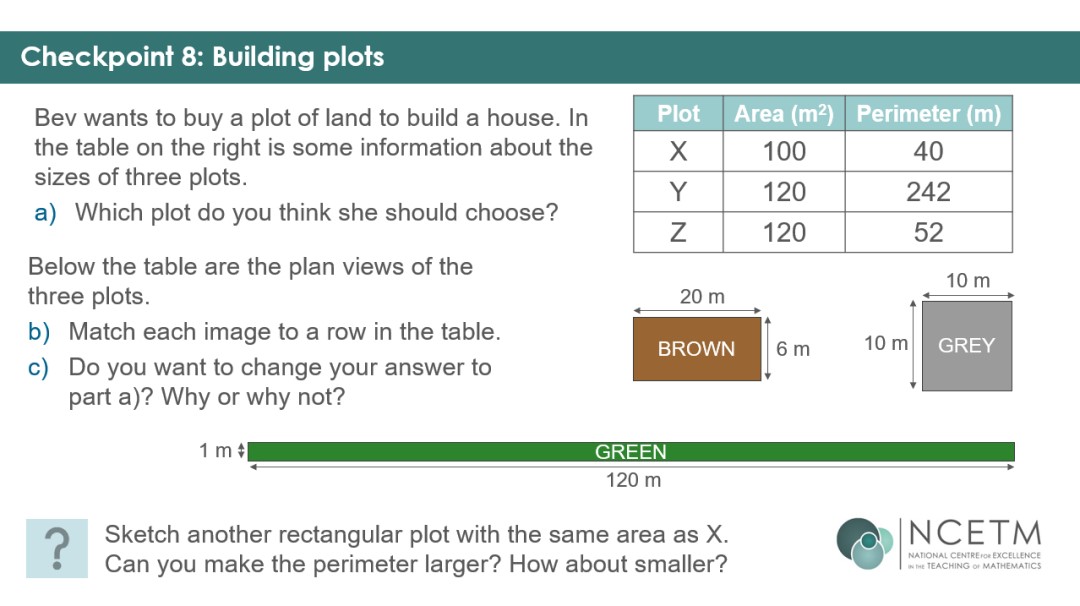
Checkpoint 8 begins to look at limits of perimeter for a given area, and whether students can work with their understanding in a real-life context. The plan views don’t appear until students have had a chance to consider question (a).

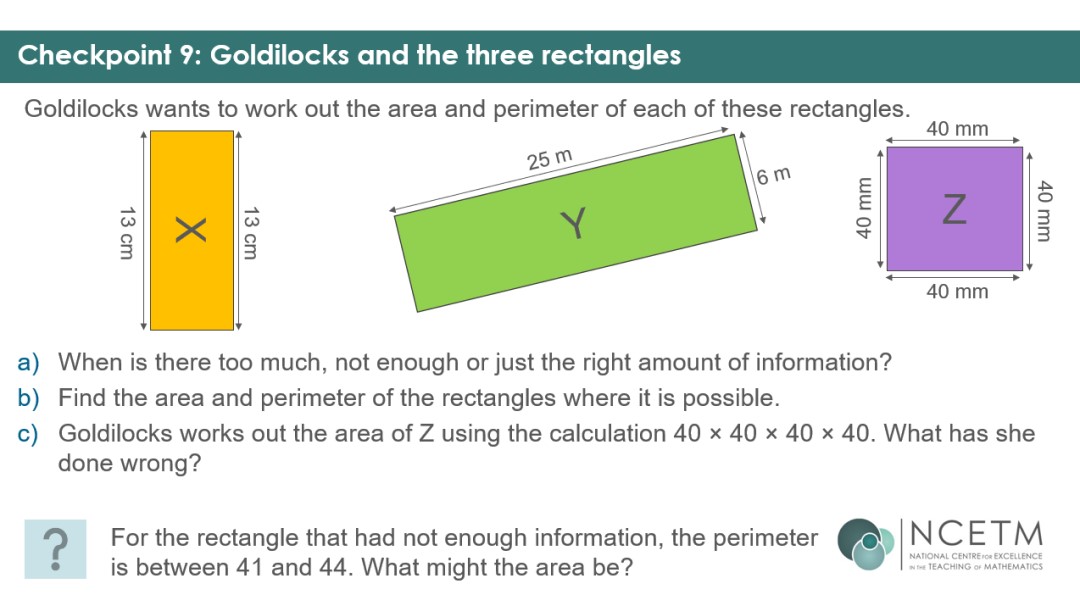
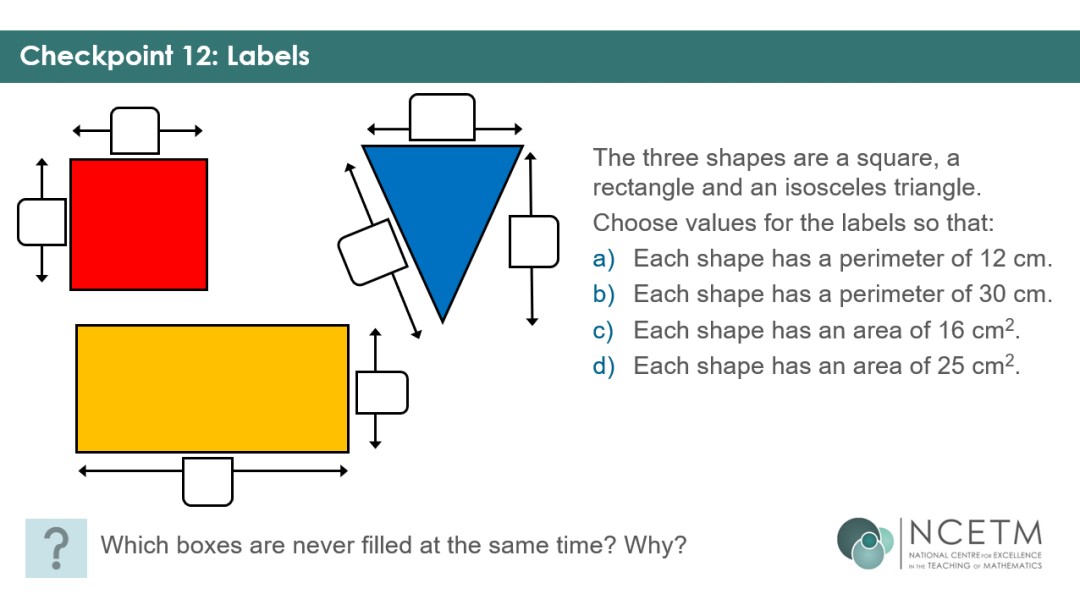
Checkpoint 9 allows you listen for students using over-simplified ideas such as ‘add for perimeter’ and ‘multiply for area’, giving them the opportunity to show you whether they know what information is required for each calculation.

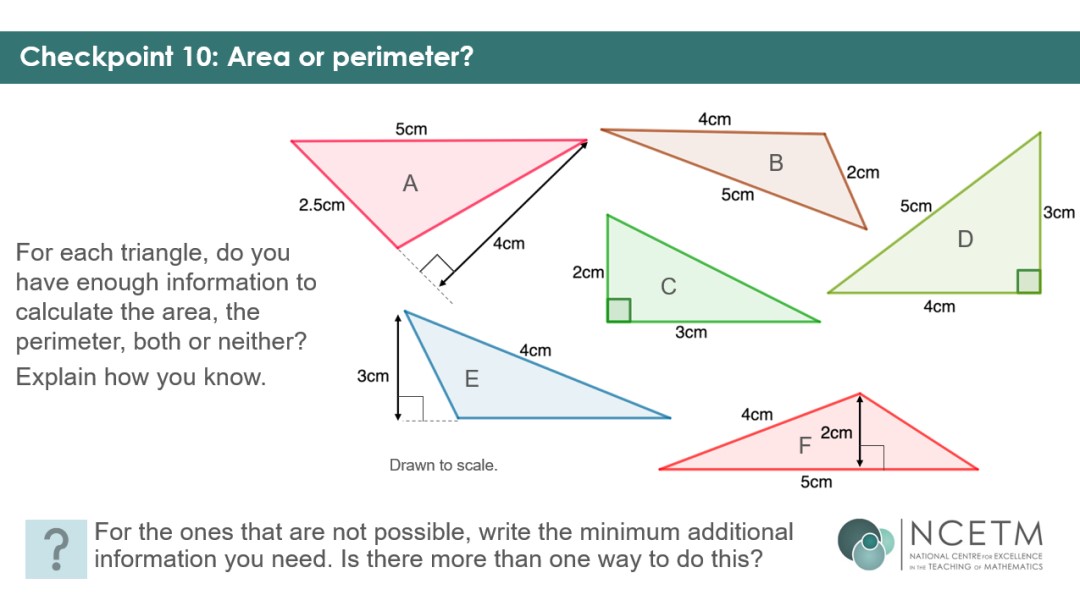
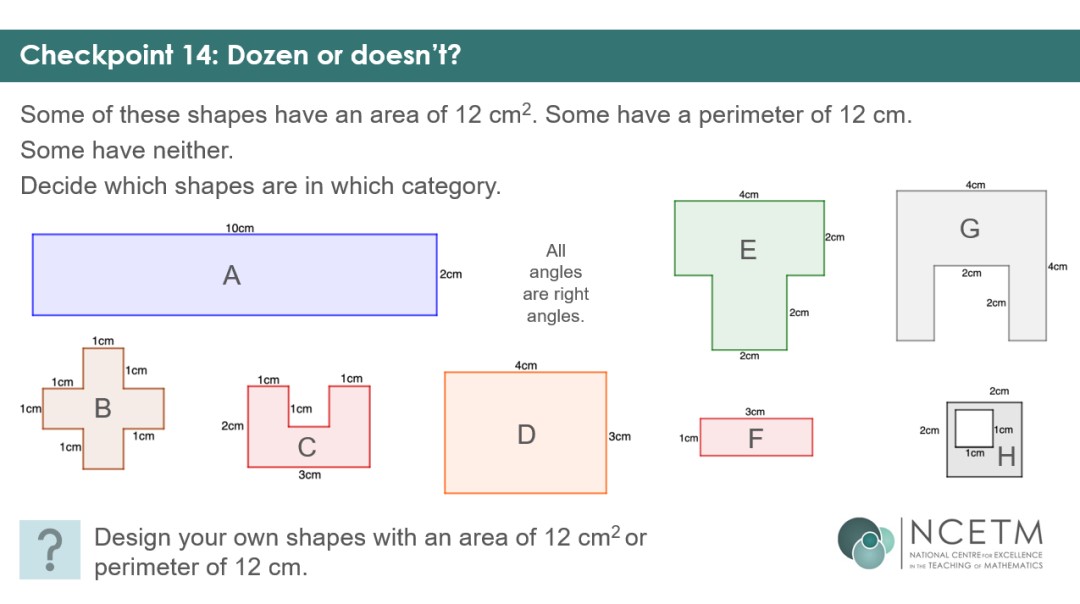
The remaining five Checkpoints ensure that students can use their understanding of the concepts flexibly by presenting them with different shapes – triangles, parallelograms and compound rectilinear shapes. Students should have worked with triangles and parallelograms in primary school, and it will be useful to see how robust that understanding is, and what they remember. Working with area and perimeter simultaneously will allow you to assess whether students are still confusing the two concepts.

Both perimeter and area are concepts that students should have worked with at primary school. So now when your Year 7s tell you ‘oh yes, we’ve done area and perimeter’, Checkpoints provides activities and resources to allow you to find out just how deep their understanding of the concepts is?

When a student has a deep understanding of area and perimeter, there should be no chance to confuse the two, and they have a fighting chance of being able to work out the formulae without recourse to a memorisation.