The Five Big Ideas at Secondary – Variation
What do we mean by variation in the secondary classroom?
20/11/2025

Continuing our series on the Five Big Ideas at Secondary, we chat to Richard Perring, Associate Deputy Director for Secondary, about variation. He explains how variation fits in with the other Big Ideas, and gives examples of how to think about variation in your planning. Find out more about the Five Big Ideas in Teaching for Mastery.
What do we mean by ‘variation’?
People talk about two different types of variation: procedural and conceptual. Fundamentally, variation is about making changes to questions and to situations that students are presented with, so that mathematical structure is exposed in some way. It gives students something to talk about, and allows the teacher to draw attention to that particular thing so that the change is intentional. It allows students to see mathematical structure, and that is the essence of what variation is.
Why is variation in maths important for teachers?
If we think about the Five Big Ideas in Teaching for Mastery, structure is explicitly named in Representation and Structure and is woven throughout the Five Big Ideas. Variation allows that mathematical structure to be accessed.
It allows the teacher and the students to notice something together, and to have an awareness drawn to something structural. It gives an opportunity then to say why has that thing happened? Why did making that change also create that other change? Why has keeping that thing the same resulted in that other thing staying the same or changing? Variation is being able to notice those differences.
For example, if we want students to appreciate that non-unit fractions are integer multiples of unit fractions, we might begin by telling them that 8/15 of 465 is 248, and ask them to find 4/15, 16/15 and 8/3. Because an ‘answer’ is provided at the start, the teacher can use variation to draw attention to the structure that the changes highlight.
How does variation fit into the Five Big Ideas in Teaching for Mastery?
It’s important to think about its relationship with structure again. When we think about Representation and Structure, representation is giving access to the structure.
- EXPLORE: The NCETM Secondary PD Materials explain how variation can help expose mathematical structures for students
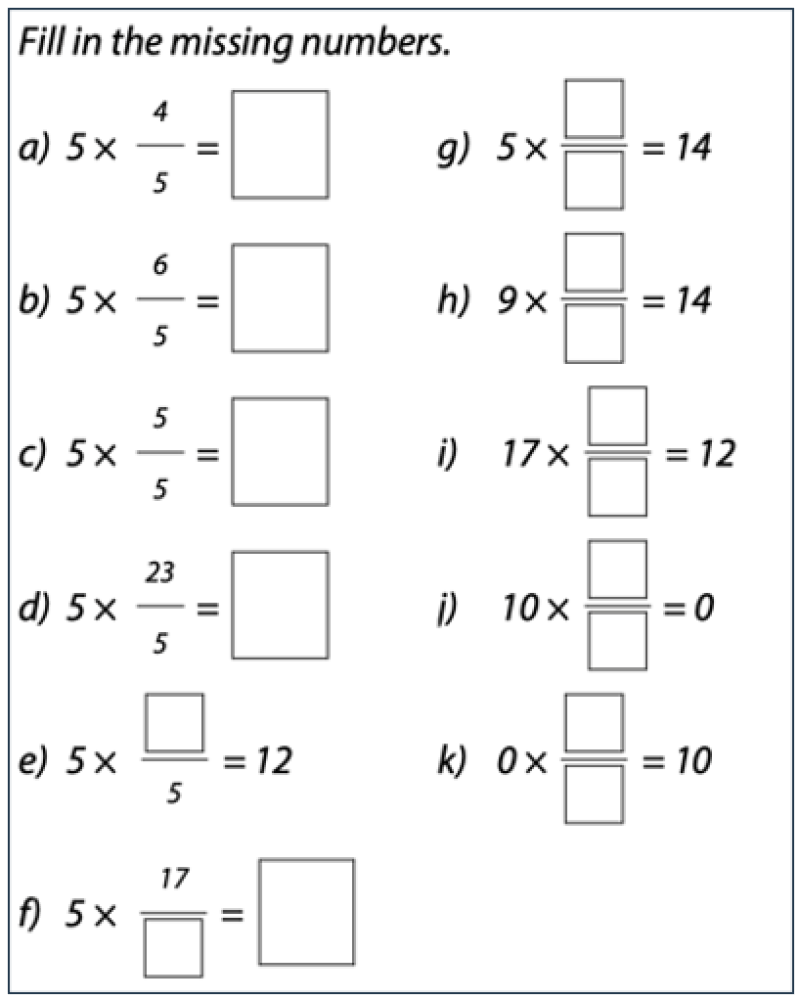
One aspect of developing fluency is having access to structural shifts. If you have a calculation and you want to work fluently with it, fluency requires flexibility. A way to develop that is to use variation, and to see what you can change and maintain within the calculation. If we want students to appreciate that any number can be transformed into another number by multiplying, we might use this task:
Anticipating how students might respond to particular variations is an important part of planning for, and teaching with, variation. If you were going to use an activity like this, as part of your planning you would consider how you would anticipate students’ responses to these questions.
How can teachers use variation when designing maths lessons?
It depends on what the teacher wants to get out of it at the time. What’s important is that when the teacher is designing the task, they need to know what they want the students to learn – this is the intended learning. They need to know what they will be drawing attention to and what the intended object of the learning is for that lesson. It’s likely to be quite fine grained; that is to say, there will be other things students might notice and explore, but there will be a key mathematical idea that they want students to understand and learn.
For each task that a teacher uses within a lesson, there might be a slightly different intended objective, but they will build and build towards a bigger picture. It might involve coming at the same concept from different angles. This is conceptual variation, and it might involve understanding what something is and what it isn’t using examples and non-examples.
If you're looking at a fraction, there are lots of things that aren't fractions. An elephant is not a fraction, but that's not a helpful non-example. You need to have boundary cases – non-examples that have some features of the example. This allows a teacher to introduce and dispel misconceptions, and tackle mistakes that students may go on to make later. The teacher's role is to be really clear and to know what they want the students to notice.
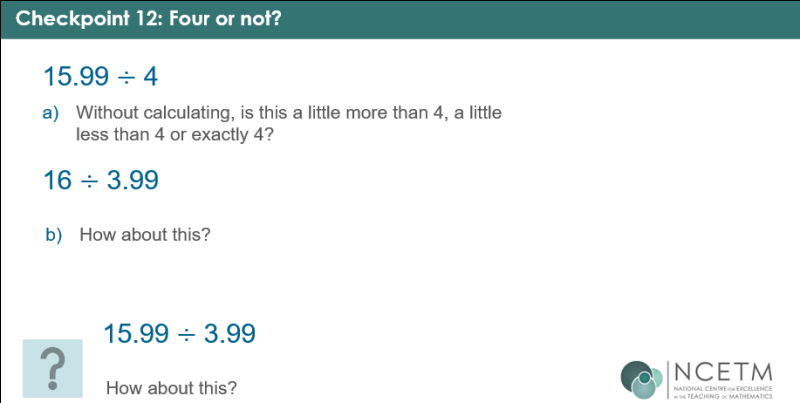
In this task, we want students to understand the impact of changing the dividend and divisor on the quotient:
As this is one of the Checkpoints slides, it also includes notes which suggest questions a teacher could ask to draw out students’ understanding:
- How does knowing that 16 ÷ 4 = 4 help here?
- Is there a ‘story’ that you can think of that helps?
- £16 shared between four people means they get £4 each. Does that help with part a? What about with part b?
- If a bag of flour weighs 4 kg, then to make 16 kg we’ll need 4 bags. Does that help with part a? With part b?
Discussing those with colleagues as part of your planning would give everyone the chance to anticipate what students might say, and prepare how to draw their attention towards the key concepts involved in estimation and rounding.
What are your top recommendations for teachers who want to improve their use of variation?
The first thing is simply to really think about it. There can be a perception that because variation is about making small changes, you can do it quite simply and straightforwardly. But it really does need thinking about, and it's always helpful to think about something with somebody else. Sharing, discussing and working collaboratively is important.
If you are already working with your Maths Hub, then you've got Mastery Specialists available who can help facilitate this sort of discussion in Work Groups. A big part of the Mastery Specialist Programme is thinking about variation and how variation supports learning, so if you've got a Mastery Specialist working with you, or if you're part of a Teaching for Mastery Work Group, you’ll get plenty of chance to look at variation.
If you’re planning on your own or with departmental colleagues, pick a mathematical concept and an intended objective of learning. Write down a set of representative examples – make sure they include typical elements of the concept – then come up with some slightly weirder examples. Come up with some unusual and peculiar examples, then some non-examples – boundary cases. You might start with what a fraction is, and you could try what's an equation or what's a quadratic equation. Thinking about those typical, unusual and non-examples is an interesting professional development task.
To find out more about the Five Big Ideas, and to discover how your department can use variation to plan an effective maths curriculum, contact your local Maths Hub or explore some of the professional development available.
Now watch the explainer video, Why is variation one of the Five Big Ideas in Teaching for Mastery?
Did you enjoy this?
Read our other Five Big Ideas features: