The Joy of Cancelling!

How would you divide 120 by 15? The ‘bus stop’ method doesn’t work well, because 15 doesn’t go into 12 and you are back where you started. My daughter once asked me about this, which led to a discussion about the connection between division and fractions, using factorisation and equivalent fractions as a way of simplifying division sums through cancelling:

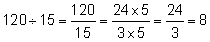
(another way of looking at it we came up with was ‘how many quarter hours are there in 2 hours?’, which works well for these particular numbers). The links between division and fractions, and the use of cancelling, are very important ideas for developing fluency with numbers, and moving on to algebra and working with algebraic fractions.

A nice question using this idea is ‘How many weeks is 10! seconds?’ [no calculator allowed]. This can be accessible for from upper KS2 onwards, provided you explain that:

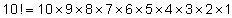
It gives a neat result that seems rather surprising.

Related to this is considering how many ways there are to arrange 10 different pupils in a queue. If you could make one arrangement every 10 seconds, how long would it take to make them all? If you wrote down one arrangement on each line of a school exercise book, how many books would they fill? Visualising large numbers is a very useful skill.

The ability to use cancelling is an important aspect of ‘mathematical fluency’, one of the aims of the new National Curriculum, and the problems above involve both ‘mathematical reasoning’ and ‘problem solving’, the other two National Curriculum aims. Mathematical fluency is a hard thing to define, involving both conceptual understanding and procedural knowledge. A nice definition, cited by Lynne McClure, the director of NRICH, at a recent NCETM event, is that mathematical fluency is the ability to use mathematics efficiently, accurately and flexibly [Russell, 2000]. I think that captures it well.