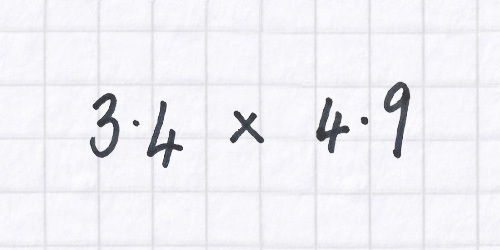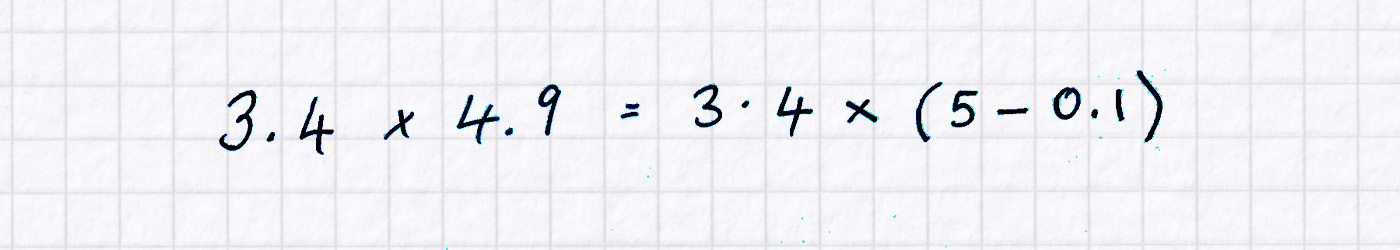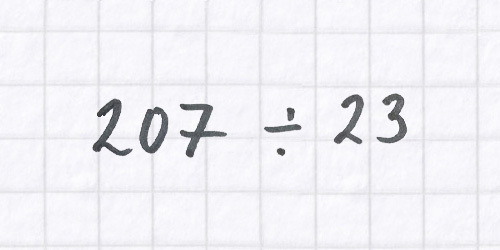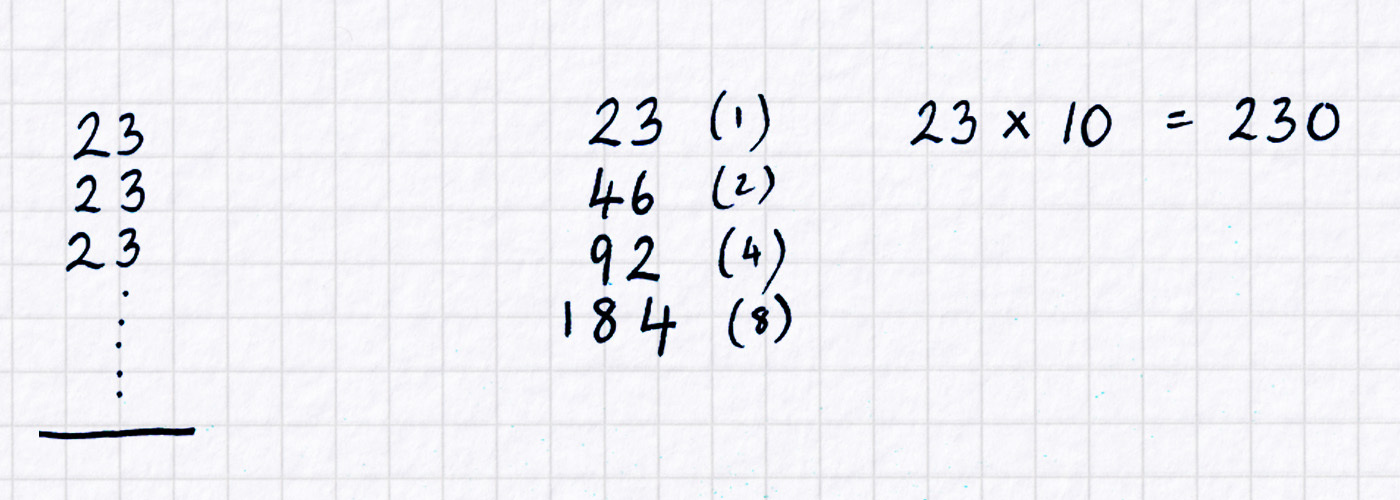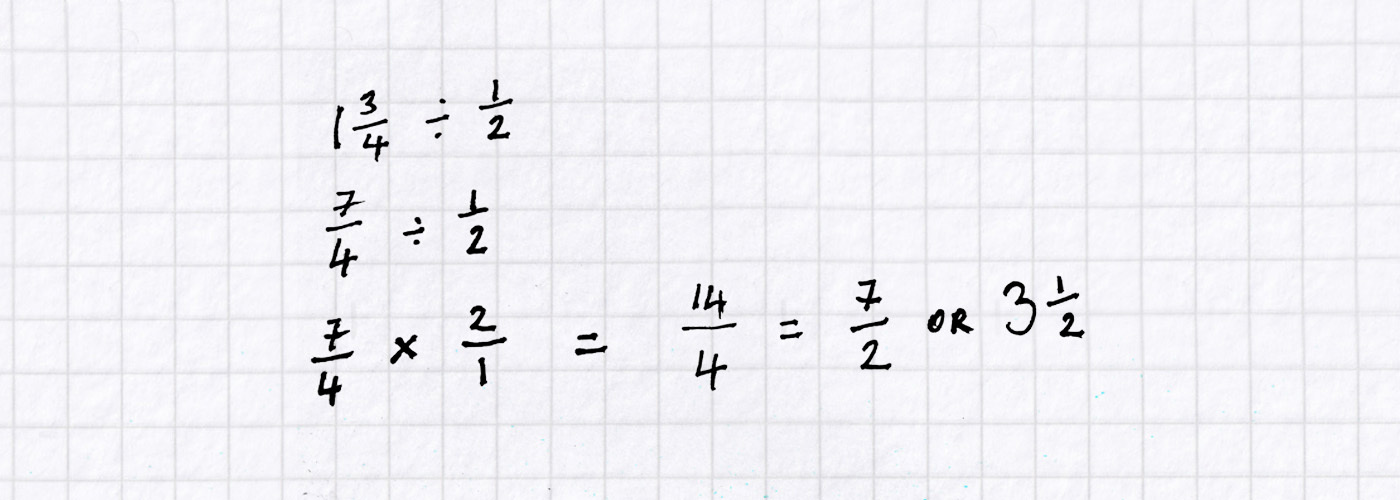Three calculations to encourage and support fluency
Prompts for teachers to draw out mathematical thinking in KS2 or KS3 pupils
06/02/2023
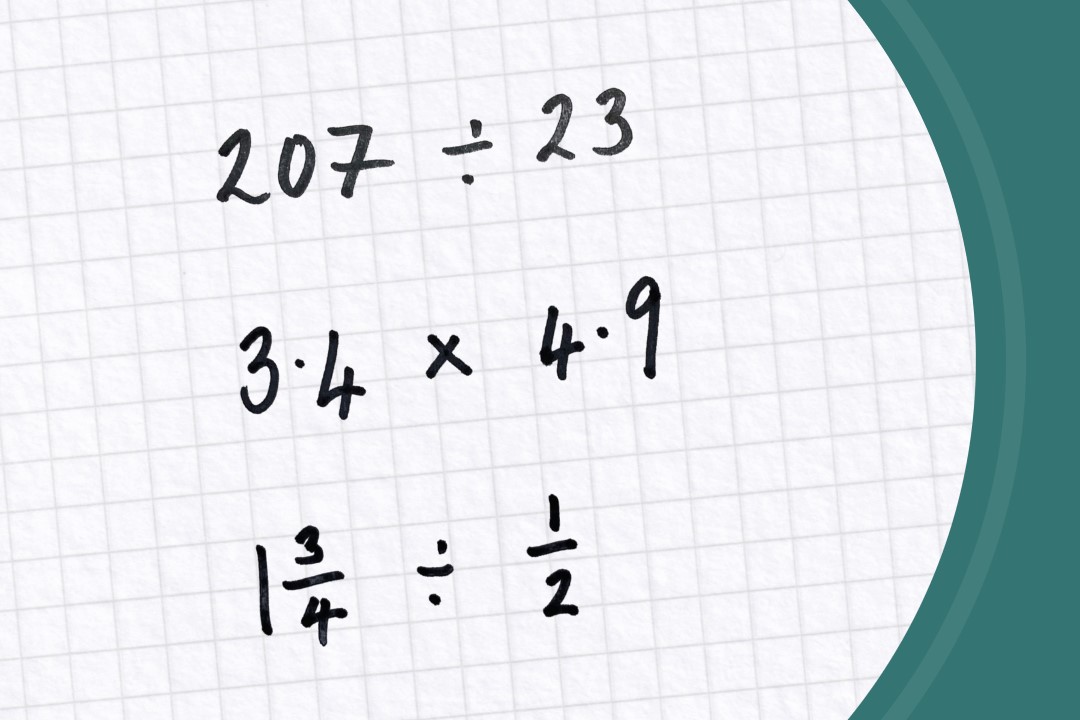
One of the beauties of maths—for those who teach it and those who learn it—is that a few simple digits and symbols on a board at the front of a classroom can open up a rich seam of thinking and discussion. Experienced teachers know that, even for outwardly simple calculations, the value for pupils lies not just in ‘getting the right answer’ but in seeing, explaining and discussing a range of ways that calculations can be approached. In the three examples below, it’s not our intention to suggest how teachers should approach them with pupils. And we’re certainly not suggesting that the approaches we mention are the only ones. We simply hope that the observations and comments will prompt thought and discussion among you and your colleagues, and perhaps indirectly help you stimulate rich discussion in a primary or secondary classroom sometime.
Question 1
This example throws up several factors, including: decimal points, the value of making an estimate before doing any calculation at all, efficient methods of multiplying two-digit numbers, and thinking algebraically.
Decimal points
Many teachers would see the decimal points and think that’s what will trip up many of my pupils. So, one strategy is to remove them both, calculate 34 × 49, and then put a decimal point back in the answer. But where to put it back? An estimation of the answer, made before putting pen to paper, will help.
Estimation
Making a rough estimate of what an answer is likely to be is a good way of spotting answers that are wildly wrong. Here the multiplication is ‘about 3 times about 5.’ So, the product is not going to be far away from 15.
Putting the decimal point back in
Whether using the column method or other approaches to multiplying two-digit numbers, the result of multiplying 34 by 49, if no mistakes are made, will be 1666. So, thinking back to our estimate, the only place for the decimal point to be re-inserted is between the first 6 and the second 6, giving an answer that is ‘not far away from 15,’ i.e. 16.66.
A more fluent method?
Some pupils in some classes might spot, maybe with a little prompting, that 4.9 is very close to 5 (a much easier number to handle than 4.9) and do some thinking in their heads that re-expresses the calculation as ‘3.4 times 5, minus a tenth of 3.4.’ Expressed algebraically—your choice whether to use this description—this would look like
From here, with care and clear thinking, the calculation can be done mentally. The thinking might go like this:
(i) Let’s do five times 3.4 first. I know ten times 3.4 is 34, so five times 3.4 is half 34, which is 17.
(ii) Now I have to subtract, from 17, a tenth of 3.4, which is 0.34. 17 minus 0.34 is 16.66.
Question 2
This is an example of where the formal written method of division (the ‘bus stop’ approach—perfectly efficient for many calculations) isn’t any help, because 23 doesn’t ‘go into’ 2 or 20. So we’re back at square one.
After that realisation, a very helpful first step - using a quotitive or grouping model for division - is to see this as asking us 'how many 23s are there in 207?’
Pupils will then approach the task in different ways, probably with jottings, possibly including these approaches. The word ‘chunking’ might even be heard somewhere.
And, as ever, arithmetic slips will be the main enemy here.
The neatest, and speediest, method will probably start with seeing that ten times 23 (230) is close to the ‘target’ number of 207. But what happens in the brain during the step that ends with seeing that 9 times 23 is 207 must vary wildly from pupil to pupil, as it does from teacher to teacher. So, getting a few pupils to try to articulate their thoughts would be a very interesting and fruitful exercise for everyone in the room.
Question 3
Pupils may have encountered methods for dividing by fractions which involve multiplying by the reciprocal of the divisor, but not necessarily made sense of why these calculation are equivalent. Their workings might look like this:
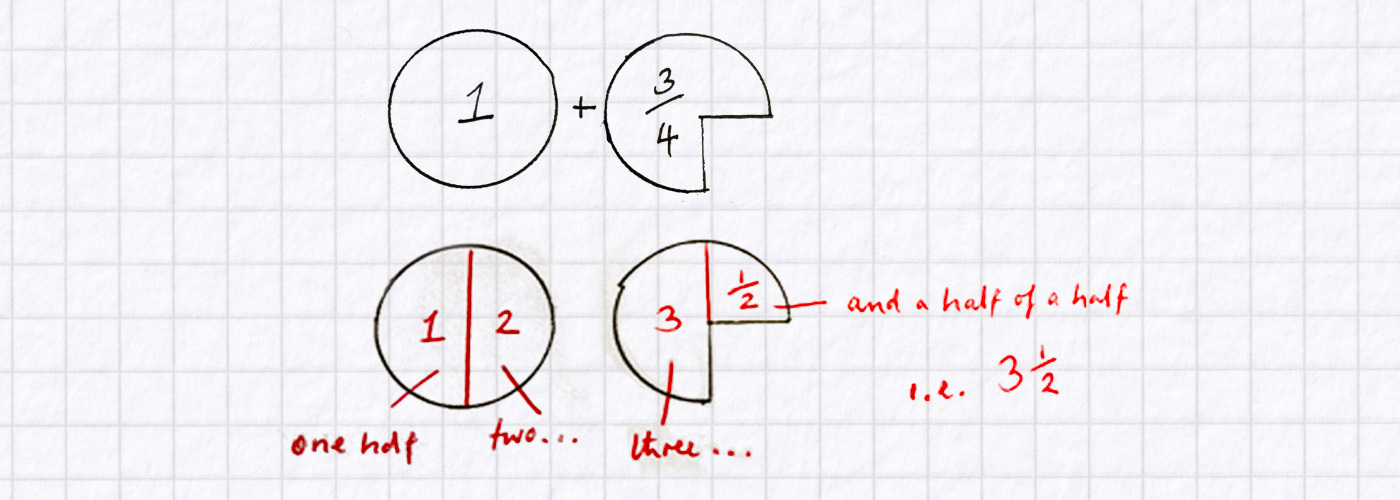
Whether or not pupils have been taught a method/algorithm to handle division of fractions, a good way to start making sense of this sort of calculation is to put into words what the division symbol is asking us to do. One way of interpreting this, using the quotitive model of division again, is how many halves are there in one and three quarters? Formulating, and thinking about, that question might be enough for some pupils to do the calculation in their heads. Others, though, might find a diagram helpful. Here’s one of many possible sketches that might help.
The image above could be used alongside a known method, to ‘sense check’ their answers. Or, more importantly, to draw pupils into a discussion of why their method works. It’s not magic, after all, is it?
Acknowledgement
We’re claiming no originality in the choice of the three examples above. They were, in fact, used by Gwen Ineson and Sunita Babbar, from Brunel University, in a recent session with NCETM staff members. You can read a related chapter, part of a wider publication, by the two Brunel academics in Mental maths: just about what we do in our heads?.
<p>Professional development</p>
<p>Our primary and secondary Mastery Professional Development Materials are full of prompts for teachers to support mathematical thinking.</p>
Explore