Understanding multiplicative relationships

"The concept of a multiplicative relationship – that any two numbers can be linked by a multiplication – is something that kids often find quite hard."
Pete Griffin, NCETM Assistant Director (Secondary).

Ask a Year 7 or 8 class how the two numbers 3 and 6 are linked, and some will probably answer that you get the second number by multiplying the first by 2. But ask the same class how the numbers 3 and 5 are linked and you may not get any answers that identify a multiplicative link. Not only is there one, but, in addition, the value of the multiplier will be related to the two numbers 3 and 5. And the relationship is that is you get the second number by multiplying the first by , or, put another way, by 1 and two thirds.

This fact, that any two numbers can be linked by a multiplier, is the starting point for the entire area of mathematics known as multiplicative reasoning. And multiplicative reasoning is one of the six broad themes of our new Mastery Professional Development Materials for KS3.

It’s also a theme mentioned in some depth in a podcast episode we’ve recently published, where the authors of the materials talk about how they see teachers using them. The quote at the top of this article, from Pete Griffin, one of the NCETM’s Secondary Team, is taken from that podcast.

In the materials themselves there are plenty of examples of tasks that could be used within lessons to draw out and deepen students’ understanding of key ideas. Perhaps more important, though, the materials can be used to prompt discussion among teachers planning sequences of lessons, or to support some deep thinking in a maths department about how certain mathematical ideas might be taught.

To give you a flavour, here are some of the examples from the multiplicative relationships section of the materials.

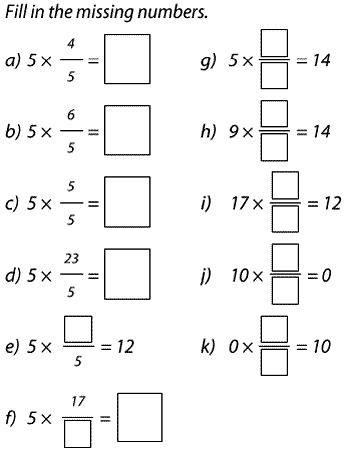
The commentary alongside this example draws attention to the carefully designed order of these 11 questions. They move from requiring the performance of a multiplication to finding a multiplier that will produce a required product. There are also suggestions of what teachers might ask students to discuss and explain, for example the link between the answers in a) and b) and the numerator of the fractions. Similarly, f) could prompt discussion of the number of possible solutions.

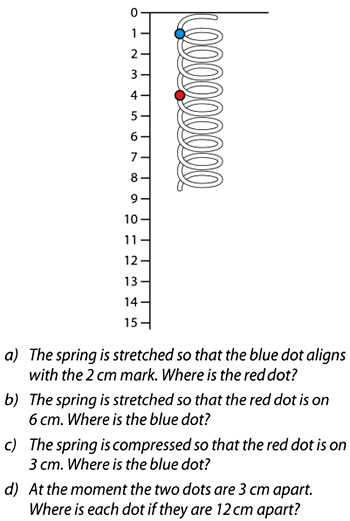
This question illustrates the link between scaling (up or down) and multiplication. The commentary in the materials suggests that, before students attempt to answer the questions, teachers encourage thought and discussion about whether the two dots will stay the same distance apart when the spring is stretched.

Alongside this example, and dotted around all these materials, is a prompt inviting teachers to consider what questions they might ask to draw out deep understanding. The suggestions here are these:

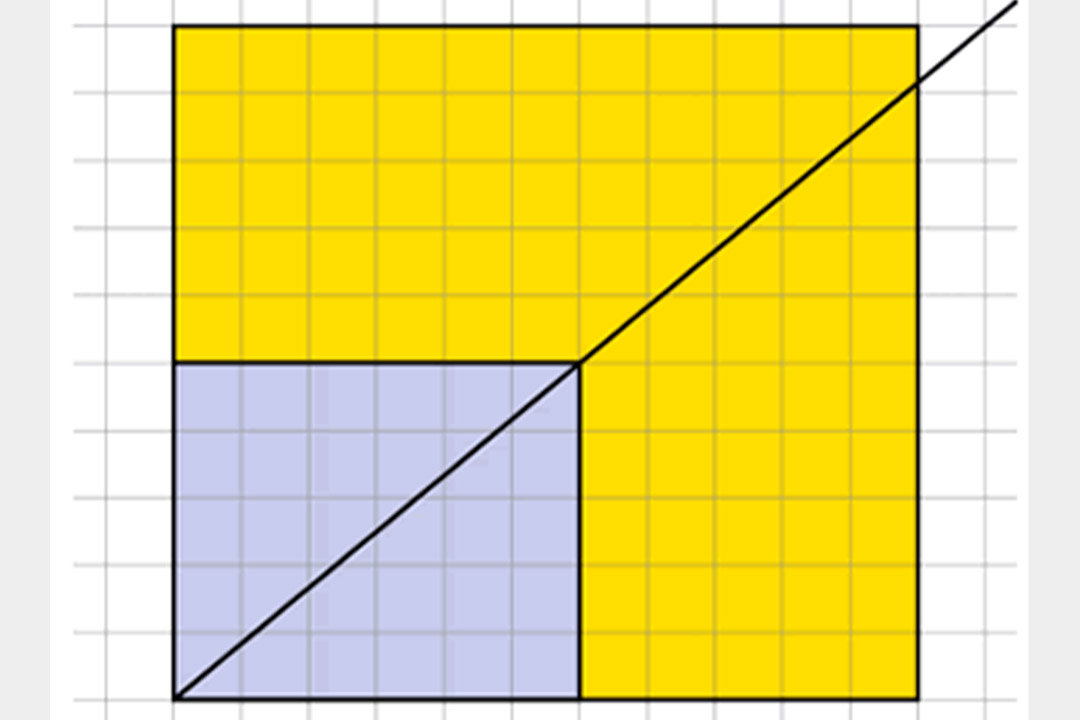
Another feature of the materials is the frequent reference to misconceptions commonly displayed by students. A case in point is the example below, which links the ideas of enlargement and proportion.

A common misconception from students faced with this question is that, because both dimensions of the smaller square have been increased by adding 5 units, then the two rectangles are similar. They are, of course, not similar because each dimension has not been increased by the same multiplier.

By drawing a diagonal through the smaller rectangle and extending it as shown below:

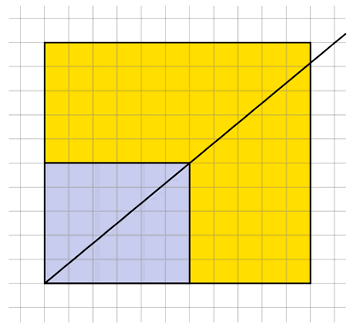
… it can be shown the two rectangles are not in proportion, and this image lays the foundation for important later work on and the constant of proportionality.

The above examples are just a few of numerous tasks in multiplicative relationships section of the materials. But we hope they’ve given you a taste of how they might be used by you and colleagues in your department.