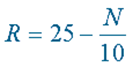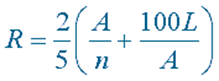- National Curriculum Tool
- Year 6 - Algebra
Year 6 - Algebra
New Curriculum
- use simple formulae
- generate and describe linear number sequences
- express missing number problems algebraically
- find pairs of numbers that satisfy number sentences involving two unknowns
- enumerate possibilities of combinations of two variables
Non-Statutory Guidance
Pupils should be introduced to the use of symbols and letters to represent variables and unknowns in mathematical situations that they already understand, such as:
- missing numbers, lengths, coordinates and angles
- formulae in mathematics and science
- arithmetical rules (e.g. a + b = b + a)
- generalisations of number patterns
- number puzzles (e.g. what two numbers can add up to)
Links and Resources
Making Connections
Mathematics is an interconnected subject in which pupils need to be able to move fluently between representations of mathematical ideas. The programmes of study are, by necessity, organised into apparently distinct domains, but pupils should make rich connections across mathematical ideas to develop fluency, mathematical reasoning and competence in solving increasingly sophisticated problems. They should also apply their mathematical knowledge to science and other subjects.
Connections within Mathematics
Making connections to this topic in adjacent year groups
Year 5 – Number and place value
- count forwards or backwards in steps of powers of 10 for any given number up to 1 000 000
- interpret negative numbers in context, count forwards and backwards with positive and negative whole numbers through zero
- solve number problems and practical problems that involve all of the above
Notes and guidance
They should recognise and describe linear number sequences, including those involving fractions and decimals, and find the term-to-term rule.
Year 5 – Multiplication and division
- solve problems involving addition, subtraction, multiplication and division and a combination of these, including understanding the meaning of the equals sign
- solve problems involving multiplication and division, including scaling by simple fractions and problems involving simple rates.
Notes and guidance
Distributivity can be expressed as a(b + c) = ab + ac in preparation for using algebra.
Year 5 – Measurement
- measure and calculate the perimeter of composite rectilinear shapes in centimetres and metres
- calculate and compare the area of squares and rectangles including using standard units, square centimetres (cm2) and square metres (m2) and estimate the area of irregular shapes
- use all four operations to solve problems involving measure (e.g. length, mass, volume, money) using decimal notation including scaling.
Notes and guidance
Pupils calculate the perimeter of rectangles and related composite shapes, including using the relations of perimeter or area to find unknown lengths. Missing measures questions such as these can be expressed algebraically 4 + 2b = 20 for a rectangle of sides 2 cm and b cm and perimeter of 20cm.
Making connections to this topic in adjacent year groups
Key Stage 3 – Algebra:
- read and interpret algebraic notation
- express known relations, including spatial generalisations, algebraically using accurate notation, including prioritisation of operations
- recognise an arithmetic progression, and find the nth term
- interpret mathematical relationships both algebraically and graphically.
- use formulae by substitution to calculate the value of a variable, including for scientific formulae
- begin to model simple contextual and subject-based problems algebraically
General guidance
- When discussing different mental calculation methods:
- explore with pupils the structure behind them;
- invite pupils to make up similar examples;
-
model how these structures might be recorded using algebra and encourage pupils to record them using letters or other symbols.
e.g. 4 × 27 = 4 × 20 + 4 × 7
or 4 × 27 = 4 × 25 + 4 × 2
or 4 × 27 = 4 × 30 + 4 × -3
leading to 4(x + y) = 4x + 4y or a(b + c) = ab + ac
-
Explore ‘quick’ ways of doing calculations which rely on the algebraic structure within them.
e.g. Do this calculation as quickly as you can;
173 – 35 + 36
Write down a few more calculations like this (and the answers to them) which use the same idea. Be creative!
- When solving problems that involve finding an unknown quantity (e.g. a missing number in a number puzzle, a missing length or angle in a shape, etc.) encourage pupils to record it using letters or other symbols – e.g. 25 + ⬜ = 32; 180 = ? + 134; x + 9 = 23, etc.
Cross-curricular and real life connections
Learners will encounter algebra in:
Recipes or formulae such as: Child’s dose = Age × Adult dose
Age + 12
or F = 9⁄5 C + 32
Working out the reading age of a particular text – e.g.
where N is the number of one-syllable words in a passage of 150 words.
-
FORECAST formula
-
FOG index
where A = no. of words in passage
n = no. of sentences
L = no. of words containing 3 or more syllables (excluding the'-ing' and 'ed' endings).
More information on reading age formulae, can be found here
| Programme of Study statement | Activities | ||||
|---|---|---|---|---|---|
| A | B | C | D | E | |
| express missing number problems algebraically | |||||
| use simple formulae expressed in words | |||||
| generate and describe linear number sequences | |||||
| find pairs of numbers that satisfy number sentences involving two unknowns | |||||
| enumerate all possibilities of combinations of two variables. | |||||
Activity A: Racetrack and Design a board game
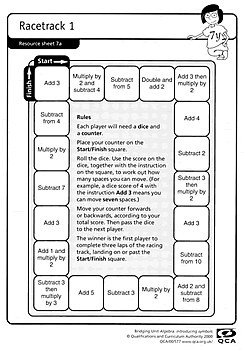
(Taken from Bridging units in mathematics – Algebra: introducing symbols, Qualifications and Curriculum Authority (QCA), 2000)
This pack of lesson materials (10 lessons for Y6 and 6 for Y7) was designed to support better continuity and progression in the learning and teaching of algebra between primary and secondary schools. The year 6 lessons contain the following themes: using function machines, notation and recording, generalising the results of an investigation and writing instructions using letters.
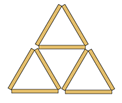
Activity B: Sticky Triangles
A puzzle in which match sticks are used to make a different number of triangles. An opportunity to generalise and symbolise.
Activity C: This Pied Piper of Hamlyn
The ‘Pied Piper of Hamelin’ is a story you may have heard or read. This man, who is often dressed in very bright colours, drives the many rats out of town by his pipe playing - and the children follow his tune.
The challenge is to investigate how many children/rats there could be if the number of legs was 600.
Follow this link for a wealth of other NRICH activities where the focus is on finding all possibilities
Activity D: Generating Sequences
Say together the three times table: one three is three, two threes are six, … Ring the multiples 3, 6, 9, … up to 30 on the grid with a red pen as you say them.
Remind pupils that multiples of 3 are numbers that divide exactly by 3 and include the numbers in the three times table.
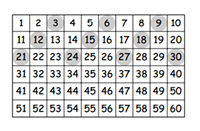
- Q Are the multiples of 3 odd or even? (they alternate)
- Q Can you describe the pattern the ringed numbers make? (sloping lines). How will it continue? (the sloping lines will extend across the grid)
- Q Will 36 be in the extended three times table? How do you know? Encourage pupils to look down the sloping lines of ringed numbers to judge whether 36 would be included. Repeat for 57 and 41.
Repeat this process for the four times table, marking them with a blue square. Draw out that all the multiples of 4 are even. This is taken from a series of four algebra lessons held on the National STEM Centre eLibrary.
The ‘Algebra 1’ lesson includes tasks on generating number sequences and describing them using formulae expressed in words.
N.B.You may wish to support the main activity of this lesson by using the ITP Number grid.
Ask:
- How many bananas are needed for 30 people going on a picnic?
- All 16 bananas were eaten at a picnic. How many people went?
- How many rugs are needed for 12 people on a picnic?
- 5 rugs were taken to a picnic. How many people went?
- How many biscuits are needed for 8 people for a picnic?
- 60 biscuits were packed for a picnic. How many people went?
- 12 hard-boiled eggs were packed for a picnic. How many people went?
The ‘Algebra 4’ lesson includes tasks on using formulae and solving simple equations
Examples of what children should be able to do, in relation to each (boxed) Programme of Study statement
find pairs of numbers that satisfy number sentences with two unknowns
enumerate all possibilities of combinations of two variables.
Children should be confident to answer questions such as;
Here are five number cards:
A and B stand for two different whole numbers.
The sum of all the numbers on all five cards is 30.
What could be the values of A and B?
express missing number problems algebraically
use simple formulae
Children should be able to express a relationship in symbols, and start to use simple formulae. For example:
- Use symbols to write a formula for the number of months m in y years.
- Write a formula for the cost of c chews at 4p each.
- Write a formula for the nth term of this sequence: 3, 6, 9, 12, 15…
- The perimeter of a rectangle is 2 × (l + b), where l is the length and b is the breadth of the rectangle.
- What is the perimeter if l = 8 cm and b = 5 cm?
- The number of bean sticks needed for a row which is m metres long is 2m + 1. How many bean sticks do you need for a row which is 60 metres long?
- Plot the points which show pairs of numbers with a sum of 9.
generate and describe linear number sequences
Children should experience activities such as;
A number sequence is made from counters.
There are 7 counters in the third number.
How many counters in the 6th number? the 20th...?
Write a formula for the number of counters in the nth number in the sequence.
-
Video material to support the implementation of the National Curriculum
This suite of videos on our website addresses the demands of the New Curriculum to introduce formal algebra into KS2.
Algebra – What’s the pattern?
This Teachers TV Key Stage Two algebra lesson starter is based around how many people can sit at a birthday party table. A single table can seat six children, one at each end and two on either side. When a second table is added, ten children can be seated (two at either end and four at each side). As the tables and the number of children grow, a pattern starts to appear. Students are challenged to work out the pattern and predict how many children could come to the party if there were 100 tables.
Chessboard Algebra
From the series ‘Great Lesson Ideas’, this Teachers TV video shows an idea for teaching algebra using a chessboard. The teacher asks her students to look for patterns in order to predict how many squares would be on different sized boards. She then presents a formula that could be used for any sized board, which the students use to test some of their predictions.
Seven Squares
A video showing how three people draw (and therefore see) this matchstick pattern of seven squares:
… and how different ways of seeing might lead to different generalisations and formulae for how many match sticks are needed for 25, 100, n squares.
Building on rich starting points
This video shows the start of a mathematics lesson at Kingsfield School where pupils are presented with data giving hints regarding a function which they then make conjectures about.
