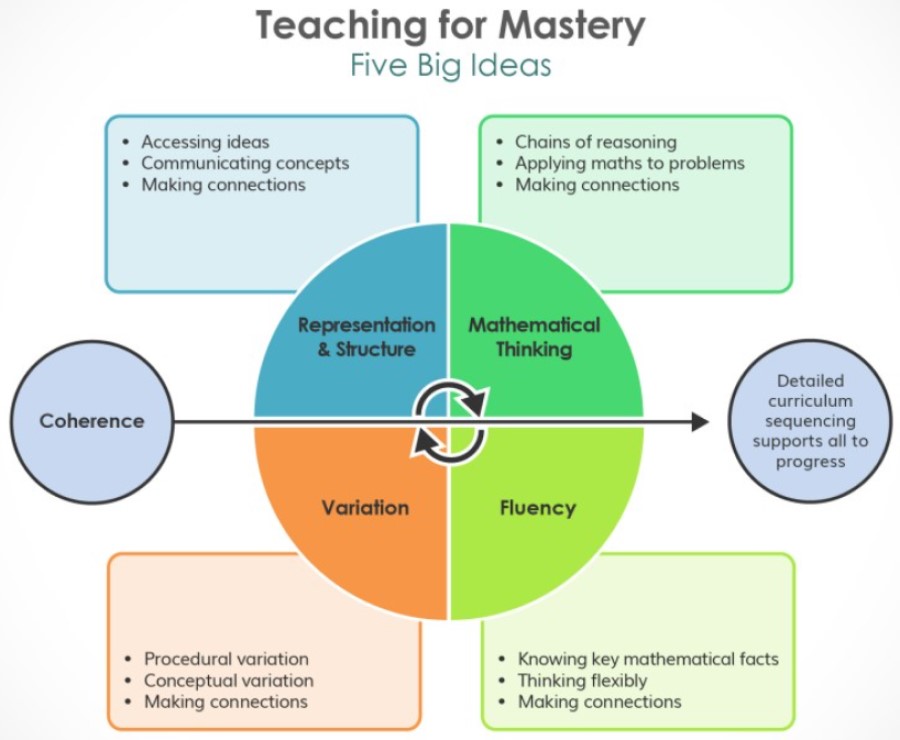
The Five Big Ideas - Representation and Structure
Discover how to use representation and structure – one of the Five Big Ideas in teaching for mastery – to improve maths teaching
24/05/2024
In this Q&A, Dr Debbie Morgan, the NCETM’s Director for Primary, explains how teachers can use representation to support children’s understanding of mathematical structures. She highlights the key dos and don’ts to remember when using this tool in the primary classroom, and shares her advice for teachers and subject leaders.
What do we mean by representation and structure?
Representation and structure are central to successful teaching and are part of a teacher's toolkit. Maths is an abstract subject – it needs to be represented in a way that allows pupils to develop their understanding, and how it is represented either prevents or provides access to mathematical structures.
Why is it representation and structure?
When we represent, we are trying to reveal the structure within a concept – how and why the maths works. Maths is about relationships; for example, when we put two quantities together, we make a larger quantity.
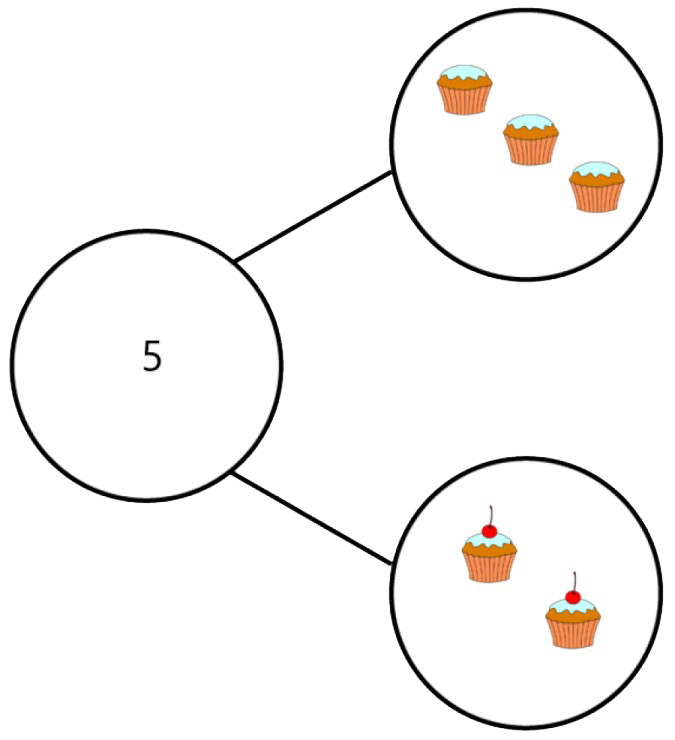
If you’ve got three cakes and two cakes and you put them together, you make a larger group of five cakes – this is an additive structure. We sometimes call this the part-part-whole relationship, and it is often represented with circles shown in a triangular structure or ‘cherry model’.
This triangular structure represents the partitioning of the whole into two parts, and we can see that the quantities inside the two circles are part of the composition of the whole. We choose to use this particular structure as it helps children understand the relationship between those three numbers.
It's important to note that we're not putting five cakes in the whole and then putting three in one of the parts and two in the other part, because then that looks like we've got 10 cakes altogether! We use dynamic movement between those three circles to show the relationship between the parts and whole.
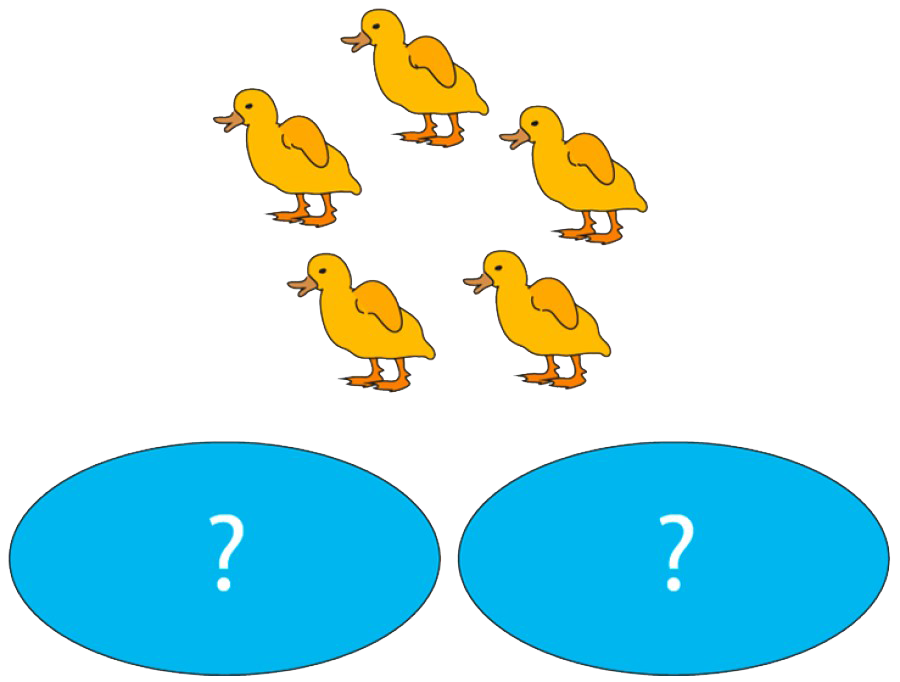
That's not the only structure we use to represent the part-part-whole relationship. In fact, at the early stages, we wouldn't want to show the ‘cherry model’ of three circles, because it is quite abstract. Teachers would need to use a real context, such as five ducks deciding which of the two ponds to swim in. We're still talking about the part-part-whole structure, but we’ve not formalised it into a cherry model.
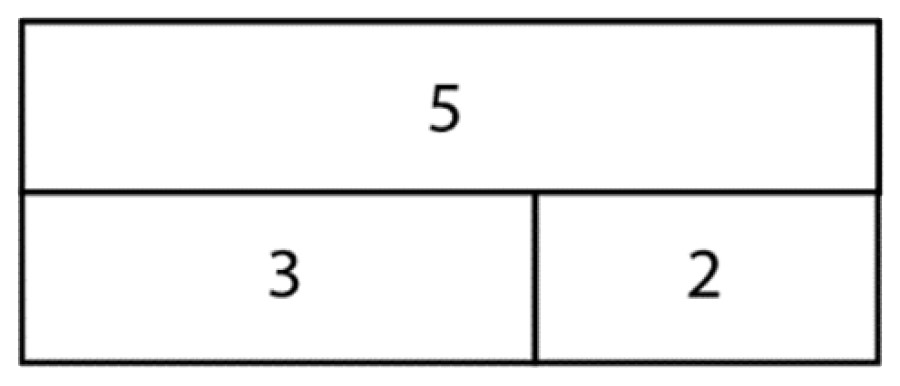
Bar models are another great tool to use when we want to draw attention to the equivalence between the parts and the whole.
Teachers should select different models to draw out certain aspects of a concept. Where the cherry model illustrates partitioning, the bar model emphasises the equivalence of five to three and two.
- LISTEN: podcast episode Using number lines in Key Stage 2
How does it fit into the other Five Big Ideas in teaching for mastery?
With representation and structure, our main aim is to stimulate children's mathematical thinking and reasoning. It links to variation because a key aspect of variation is that we represent a concept in different ways to draw out essential structures, as we did with the models above. We carefully select and order representations in a coherent manner to build and make sense of concepts and their essential features. Fluency develops in the movement between representations and the ability to see the structure of the maths represented in different ways.
How should teachers use representation and structure in their maths lessons?
I recently watched a Year 3 lesson, which was planned using the NCETM PD materials. The focus was fractions, and this was the ninth lesson in the series.
The teacher showed six bricks and one of them was a different colour – she wanted to highlight that the whole is divided into six equal parts, one of them is yellow and each part is one sixth, including the yellow brick.
Later in the lesson, the children used similar bricks to make what they called the ‘secret fraction’.
They were each given a card with a fraction on it, which they could not show to anybody else, and their task was to build a model with the bricks to represent their fraction, so their peers could guess their fraction. The children were excited about this activity, but most importantly, representing with a 3D model was helpful in deepening their understanding of the concept.
A CPA approach
Many teachers have heard of the concrete, pictorial and abstract (CPA) approach to maths, but one of the misconceptions is that it’s a linear model – we start working with the concrete, then we move onto pictorial, and finally we meet the abstract. But actually, the movement between those different representations is what is important. In this lesson, the children started working with the abstract then moved back to the concrete bricks, which gave them an opportunity to consolidate their understanding and see those links.
In this video from a Year 4 lesson, the children are exploring remainders using different representations:
- Concrete matchsticks to make shapes
- Stem sentences
- Equations.
The movement between these three models of representation, and the questions the teacher asks, embeds the learning.
The role of gesture
Schools involved in the Mastering Number Programme will be familiar with the power of gesture to secure children’s understanding. In Mastering Number at KS2, stamping is one of the key gestures we use to represent multiplicative relationships. In multiplication you have two factors which represent different things: one represents size of the unit and the other represents how many of those units there are.
For example, if we are thinking about three 50 pence pieces, the unit size is 50 and the number of units is three. We could represent it like this:
- Pretend one of your fists is a stamper
- Write 50 on the bottom of the stamper
- Stamp your fist three times whilst saying ‘50, 50, 50’.
This gesture emphasises the structure within the multiplication. From this, teachers are telling us that their pupils are easily able to draw three unitised counters of 50 and represent the maths with an expression or equation.
Here is this gesture in action:
What is the positive impact of teachers using representation and structure?
There is enormous potential. How a teacher carefully selects and represents the maths can provide those magic ‘I get it!’ moments and, as a result, children will make better progress. They'll develop deeper understanding and the ability to connect ideas together. One key thing is that structures in maths do not change. The additive structure that we reveal through the part-part-whole model is the same in Year 2 as it is in Year 12, so providing access to those structures through representations is absolutely key to all children being successful.
What are your top tips for teachers who want to improve their use of representation and structure?
Do not use too many representations, or children get overloaded. It's not about variety, it’s about carefully selecting the right representation to draw out the mathematical structure. Any that you do use, make sure you explicitly make a connection between them so pupils can see it's the same concept.
Do plan for withdrawal of the representations, as there is a danger that some pupils will get stuck using concrete objects in every lesson to help them count or calculate. The representation should not be used to calculate, but to help them see the structure.
Do make sure the numbers are not too big when using a representation. We used five, three and two as an example above as this will not cause cognitive overload. The focus here is not on calculating, but seeing how those numbers relate to each other.
Do not let children choose which representation they want to use. A child is unlikely to think, ‘I'll select this representation because it's going to expose the mathematical structure in the best way’. They'll think, ‘I like this representation because it's red’, or ‘it's shiny and I like clicking it together’. It should be the teacher's decision and all children should have the same representation, so that the focus is tight in the lesson.
Do consider implementing a set of core representations across your school if you're a subject leader. For example, a tens frame can be used in Year 1, with each counter having a value of one, and as we get towards the end of KS2, each counter may represent one tenth. Representations act as vehicles for transferring key ideas from one year group to the next.
Do recognise that staff will probably need professional development to help them to select the most appropriate representations. The NCETM PD materials discuss types of representations teachers might use and provide examples within the slides. Another helpful document is the DfE Primary Mathematics Guidance, which uses a core set of representations throughout. Get in touch with your local Maths Hub, as they offer specific CPD programmes for teachers and teaching assistants at all phases.
Now watch the explainer video which summarises Debbie's top tips for using representation and structure: