Exploring the composition of number

When a child understands the composition of number, they understand that numbers are made up of other numbers. They ‘see the numbers inside’ other numbers: first, that all numbers are made up of ones, and then that they can be made up of pairs of bigger numbers.

So for example, 5 is made of ‘five ones’, or of ‘1 and 4’, or of ‘2 and 3’.

The CBeebies' Numberblocks characters demonstrate this with their ability to split into other characters as shown as shown in The Whole of Me is Five.

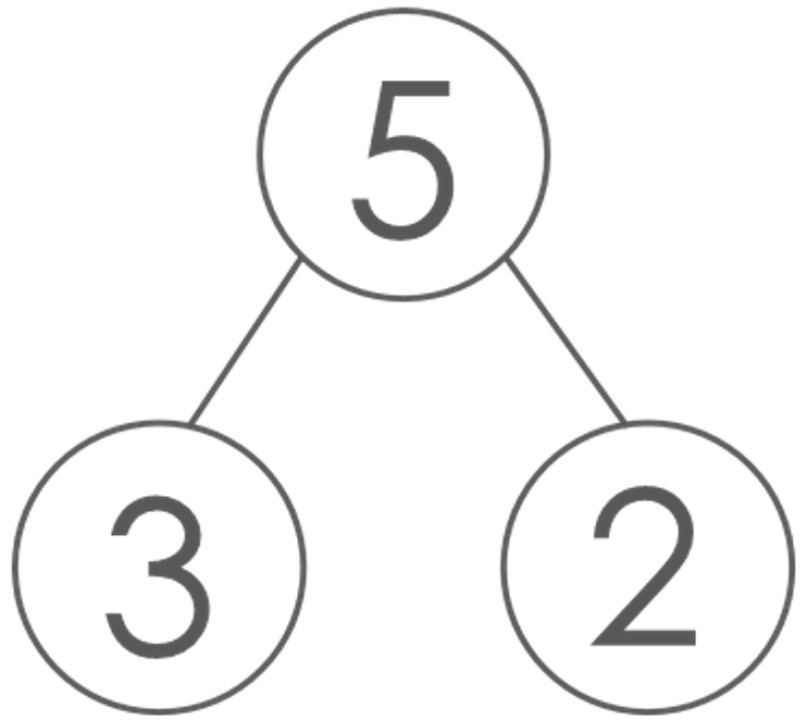
Understanding composition of number is fundamental to understanding the structure of part-part-whole relationships, which can be represented with a part-part-whole model, as below:

When 5 is partitioned into 3 and 2, then 3 is a part and 2 is a part and 5 is the whole.

The concept of composition allows children to build fluency with number bonds – not only number bonds of 10, but all the number bonds within numbers. So, back to the example of 5: number bonds of 5 are: 0 and 5, 1 and 4, 2 and 3.

Understanding composition also supports an understanding of commutativity: if you have learned that 2+3=5, then you also know that 3+2=5 without having to learn it as a new fact.

Composition is also crucial in starting to understand addition and subtraction and their inverse relationship. For those that understand composition of number, remembering that 2+3=5 and 5-2=3, and how these two facts relate, is less a matter of repetition and memorisation and more the application of structural understanding. When we add, we compose: when we subtract, we decompose.

Within the NCETM/Maths Hubs Mastering Number Programme, sessions are designed to build understanding of the composition of number for children in Reception, Year 1 and Year 2.

Different patterns of spots are used, in different arrangements, and children are encouraged to ‘subitise’ (see without counting) the smaller numbers ‘within’ the bigger numbers.

What do you see? Maybe the 4 in a square, and the odd 1?

What do you see if they are coloured like this? Probably the 2 and 3.

Children might be encouraged to say, “I know this is 5, because I can see 3 red dots and 2 black dots.”

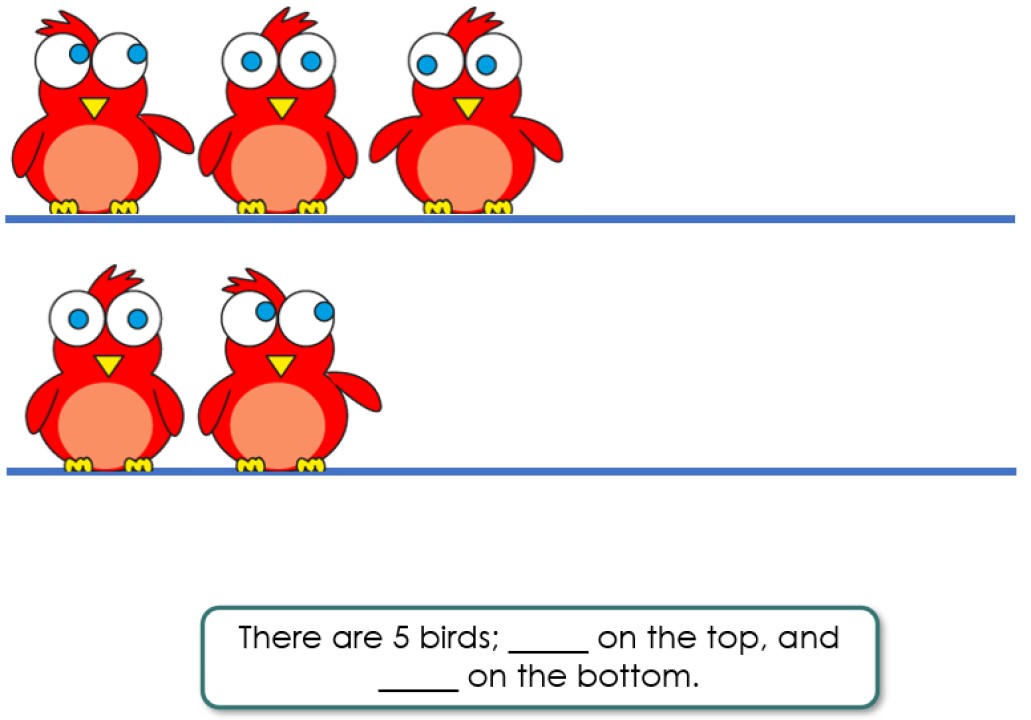
Different layouts of coloured dots within the Hungarian number frames below help develop recognition of different configurations of 3 and 2 and therefore 5.

Moving the birds between the different wires allows children to see that different pairs of numbers make 5.

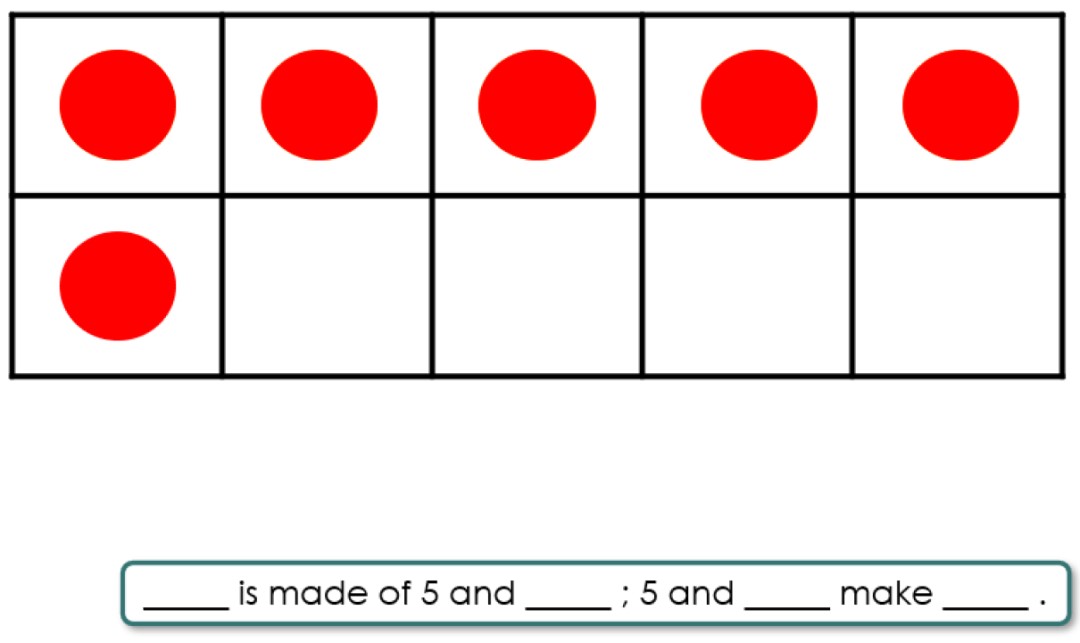
For numbers between 5 and 10, children are encouraged, again through the representations used, to see the ‘5 and a bit’ structure. Understanding numbers in relation to both 5 and 10 is important for developing efficient calculation strategies. So seeing the 5 (and a bit) in 6, 7, 8 and 9, is especially helpful.

As well as identifying that 5 is a part of the numbers 6,7,8 and 9, other bonds of these numbers are also explored separately.

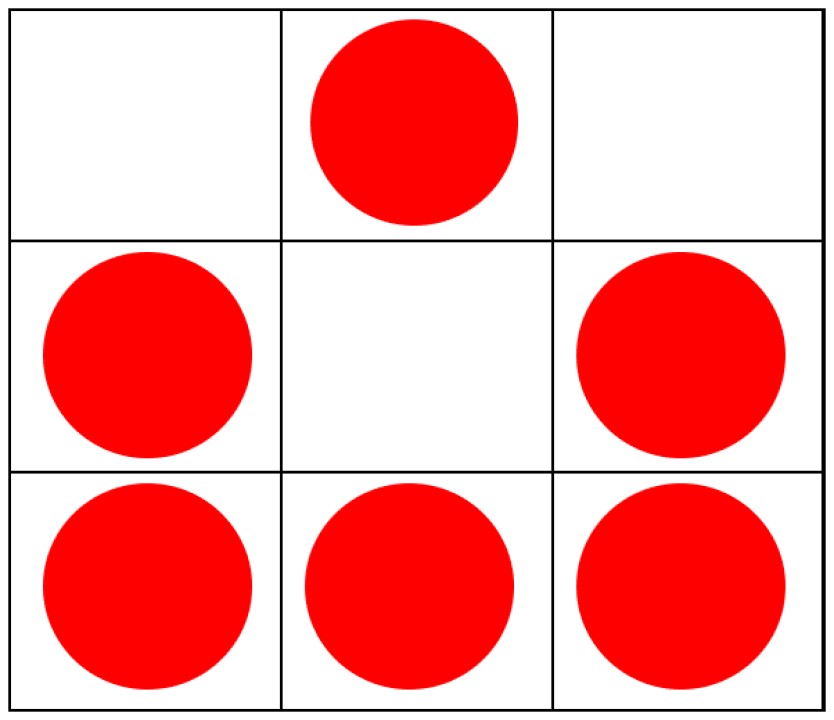
Different representations of 6 are used to expose different compositions of 6: ‘5 and a bit’, but also ‘3 and 3’, or ‘2 and 2 and 2’.

The dice pattern emphasises ‘3 and 3’:

A 9-grid allows single counters to be moved out of the familiar dice pattern to see that we still have 6. Different ways of subitising the numbers within 6 to compose 6 are explored.

The use of an eggbox allows partitioning into brown and white eggs and the use of stories about egg-laying to see the different numbers within 6.

Much more on composition, including ideas for activities, progression charts, common errors and what to look for when working with young children, is included on our Early Years page on Composition. You might also be interested in the other articles in this set, Cardinality and number sense and Teaching ordinality – more than just first, second and third.

The NCETM and Maths Hubs are considering a Mastering Number Programme for 2022/23. If you might be interested in taking part, please complete the Expression of Interest Form.