Teaching ordinality – more than just first, second and third

For many, teaching ordinality means getting children to understand and use the terms first, second, third and so on. It often gets less attention in the curriculum than cardinality (the ‘howmanyness’ of number, addressed in an earlier feature). But the DfE guidance published in 2020 strengthened the need to focus on ordinality, highlighting its importance in children’s mathematical development. Here we explore exactly what it means, and share some ideas for teaching activities to explore it in depth with KS1 pupils.

What is ordinality?

A helpful definition of ordinality (and cardinality) is given by Alf Coles, a Professor of Mathematics Education at the University of Bristol, in his 2014 paper on early number ⁽¹⁾:

Ordinality refers to the capacity to place numbers in sequence, for example, to know that 4 comes before 5 and after 3 in the sequence of natural numbers. Cardinality refers to the capacity to link numbers to collections, e.g., to know that “4” is the correct representation to denote a group of four objects.

Coles goes on to explain that ordinality is more than just learning the language of ‘first’ and ‘second’. It involves thinking deeply about the relationships between the numbers, and where they fit in the linear number system.

Why is it important?

A strong grasp of ordinality is crucial in developing number sense and fluency. It helps children improve calculation skills. For example, knowing that 49 + 32 can be calculated by thinking of the calculation as 50 + 32 - 1 is based on understanding that 49 is close to 50. Confidence with ordinality also gives a deeper understanding of how different sets of numbers work in the same way (recognising that a number line marked 0 to 10 to show whole numbers works in the same way as one marked 0 to 1 to show tenths).

The National Curriculum guidance gives ordinality its own strand (but it doesn’t use the term itself); reference to the linear number system appears in each year group. In Year 2, for example, the guidance states that children should be able to ‘Reason about the location of any two-digit number in the linear number system, including identifying the previous and next multiple of 10.’

How can you teach it?

A number line

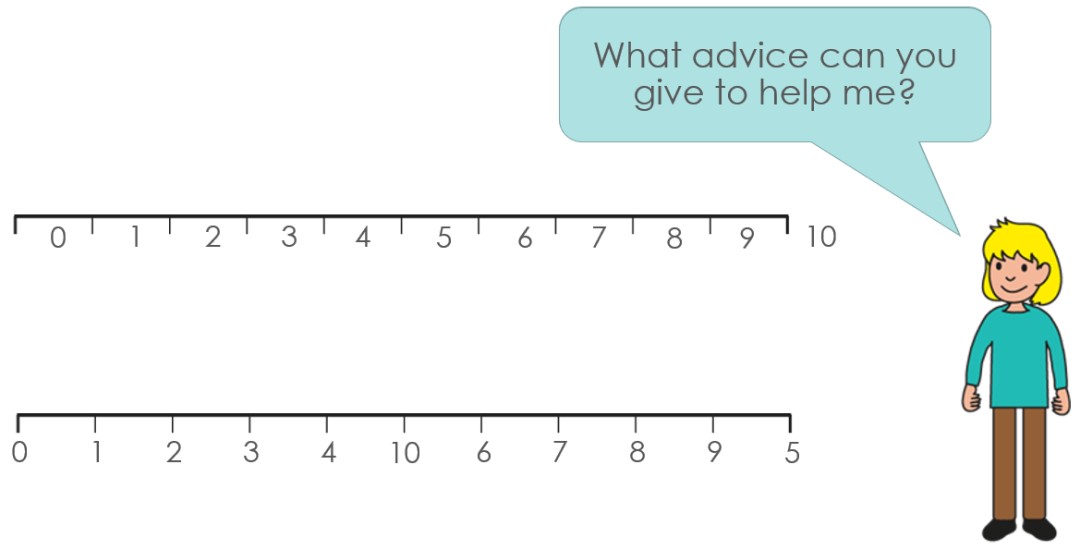
A number line forms the basis for teaching ordinality. In the Maths Hubs and NCETM Mastering Number Programme, children explore a range of number lines, including those that are marked with numbers, partially marked, and empty. Using the slide below, the teacher would ask the class ‘Are these number lines correct?’

Having elicited the response that no, the number lines are not correct, discussion would then be based around why they are not correct and how to correct them. The first number line demonstrates ordinality in that the numbers are in the correct order, but children would be encouraged to see that they are not on the marker points and that therefore the number line is not accurate. The second number line poses a different error; the numbers are on the marker points, but they are not in the correct order. Children would then discuss the correct order, using their knowledge of the linear number system.

Staircase patterns

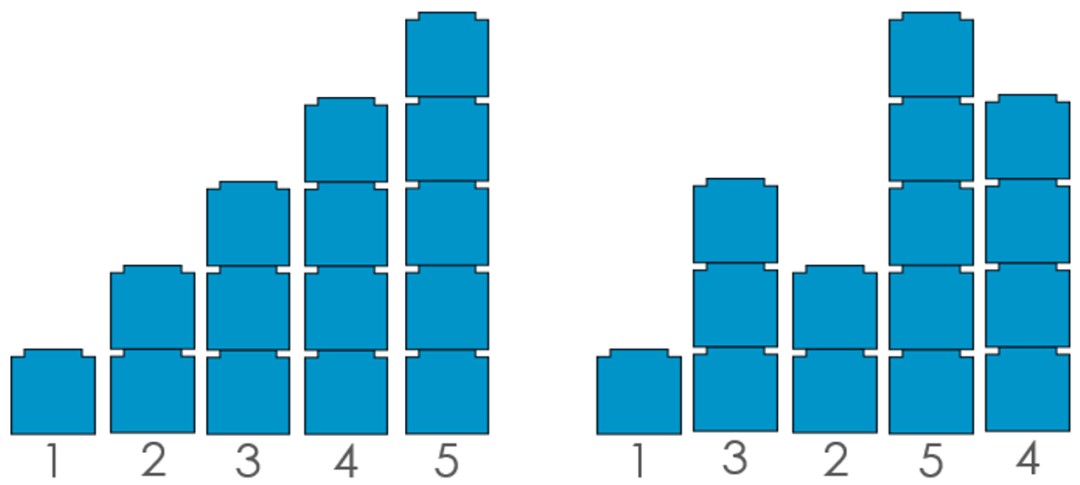
Practical activities are a great way to explore ordinality, particularly as young children love building staircases and seeing the pattern. Comparison activities also provide another opportunity for ‘purposeful provocation’ – where an adult (or a puppet) makes a mistake deliberately to promote thinking and discussion. In the example below, children are asked to compare the staircases and notice that order does matter, as the blocks in the second staircase have not been placed in the correct order. The visual element of this, either on the slide or in the staircases that children build themselves, helps illustrate the importance of the order of the numbers:

Having identified the correct order of the numbers using a staircase pattern, there is then further opportunity for children to reason about why that is the correct order. Using an example like the image below, and asking ‘WHY do the counting numbers make a staircase pattern?’, would give an opportunity to promote understanding that the number which comes before a number is one less, and the number that comes after is one more. Focusing on this specific use of language is important in developing children’s understanding of ordinality.

Rulers and objects

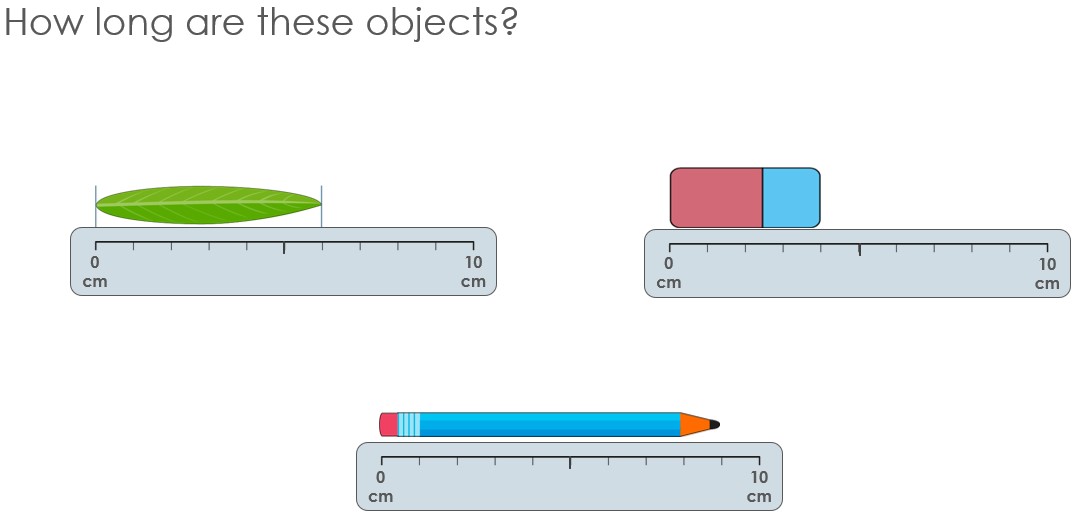
Exploring measurement is a great way to look at ordinality and where numbers fit in the linear number system as it provides a practical context. Children can explore, both through images and concrete items, how to measure an object. First, children need to understand that an object must be lined up with the zero on a ruler, and that the way to measure its length is to see how far it expands along the ruler (or number line).

The slide below shows a variety of familiar objects, and the rulers have marker points but only 0 and 10 marked, encouraging children to use their understanding of ordinality. To work out the length of the leaf, for example, children would be encouraged to reason about its length rather than count from zero. Knowing confidently that five is at the midpoint of the line, and then reasoning that the length of the leaf is ‘one more than five’, gives the answer of six.

How can you learn more about teaching ordinality?

The slides featured above are taken from the Mastering Number Programme, which is for children in Reception, Year 1 and Year 2. The programme has been running in thousands of primary schools across England since September 2021. If you would like to be involved in this programme in the future, and get access to videos, lesson PowerPoints, teacher guides, pupil resources and online CPD webinars, you can express your interest for a future cohort. Visit the Mastering Number webpage to learn more.

You might also be interested in the other articles in this set, Cardinality and number sense and Exploring the composition of number.

(1) Coles, A., 2014. Ordinality, Neuroscience and the Early Learning of Number. North American Chapter of the International Group for the Psychology of Mathematics Education.