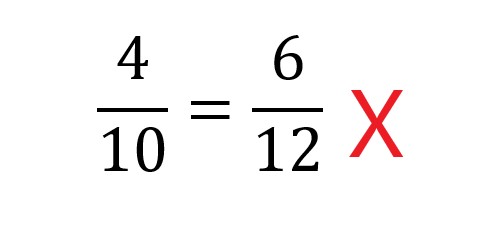Introducing multiplicative thinking

What does this image convey, and why is it important in maths?

The image, taken from the NCETM Primary Mastery Professional Development materials, is one of a series of representations built to support children in the conceptual shift from additive thinking to multiplicative thinking.

The first expression ‘2 + 2 + 2 + 2’ represents the additive relationship that children become familiar within the first few years in school.

‘4 × 2’ represents the multiplicative relationship – 4 groups of 2 children.

This shift is one of the hurdles where children can get ‘stuck’ in their mathematical learning. In a 2018 paper, two influential maths education researchers suggest:

It is likely that the concept of addition is closely related to an inborn primitive conception, (and that) the concept of multiplication is not.

If multiplicative understanding is not embedded, then progress in maths will be limited. A significant amount of maths in KS2 and beyond depends on the ability to think and reason multiplicatively. For example: fractions, ratio, percentages, trigonometry, similarity, pie charts, etc.

Any secondary teacher will tell you that even older students often think additively by default. In many contexts if you ask a student about the relationship between two numbers, they will often look first at the difference, even where the relative proportions are more relevant. For example, here is a classic mistake in equivalent fractions, made by looking at additive relationships rather than multiplicative:

In this article, we will look at how multiplicative thinking is introduced in the NCETM Curriculum Prioritisation resource, using slides that originate in the NCETM Primary Mastery Development Materials.

Introducing multiplication

Multiplication is often taught as repeated addition, so ‘4 + 4 + 4’ is regarded as 4 added to 4 added to 4. This is a worthy starting point, since the learner can relate multiplication to what should be secure addition facts and concepts. However, it is important to progress to being able to see ‘4 + 4 + 4’ as ‘three 4s’, since this indicates the beginnings of multiplicative thinking.

The 2018 paper further argues that this development in thinking cannot be taken for granted.

In human history, there is a long gap between the development of addition and the development of multiplication. For students, there is also a gap. One task of school arithmetic is to give students a pathway across that gap.

The learning sequence built up in the Curriculum Prioritisation materials (Year 2, Unit 5) gives a pathway across the gap by starting with familiar additive concepts before introducing a multiplicative way of understanding, always making links to what is already understood.

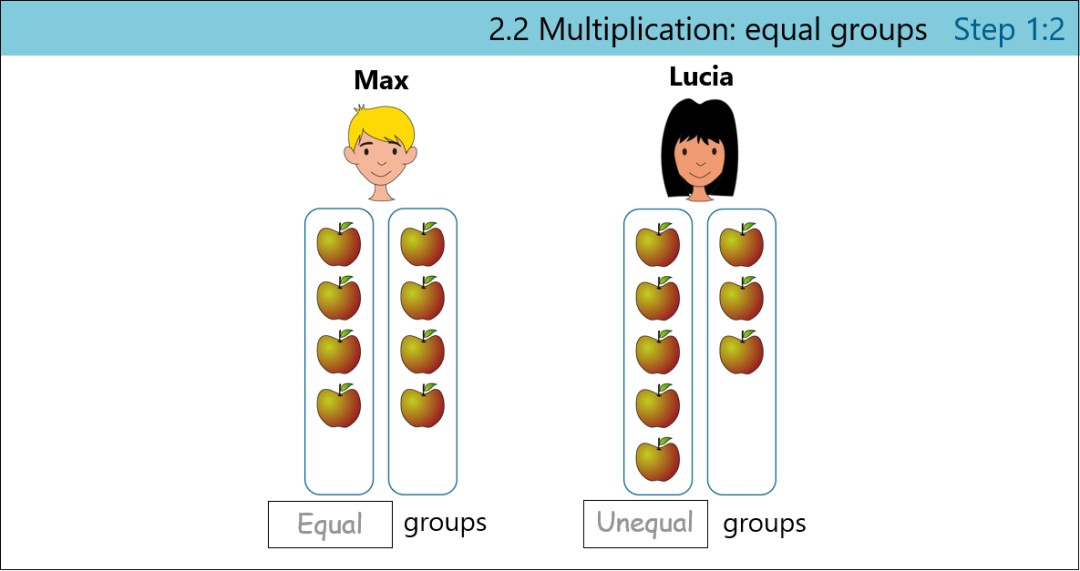
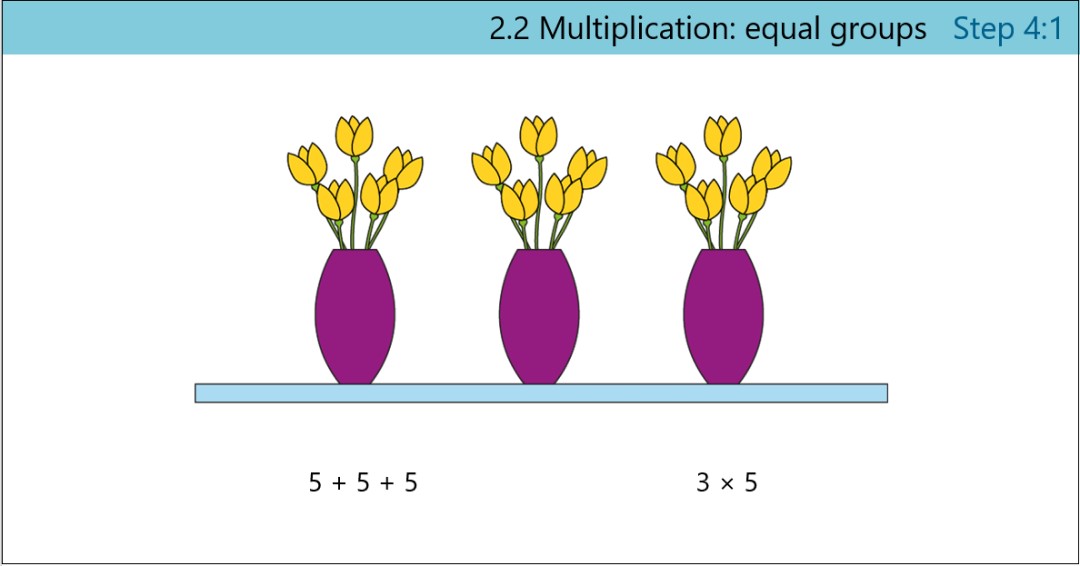
Grouping: equal and unequal groups

First children look at grouping objects, with a focus on recognising equal groups, and then describing them.

Click/tap to enlarge

Recognising equal and unequal groups

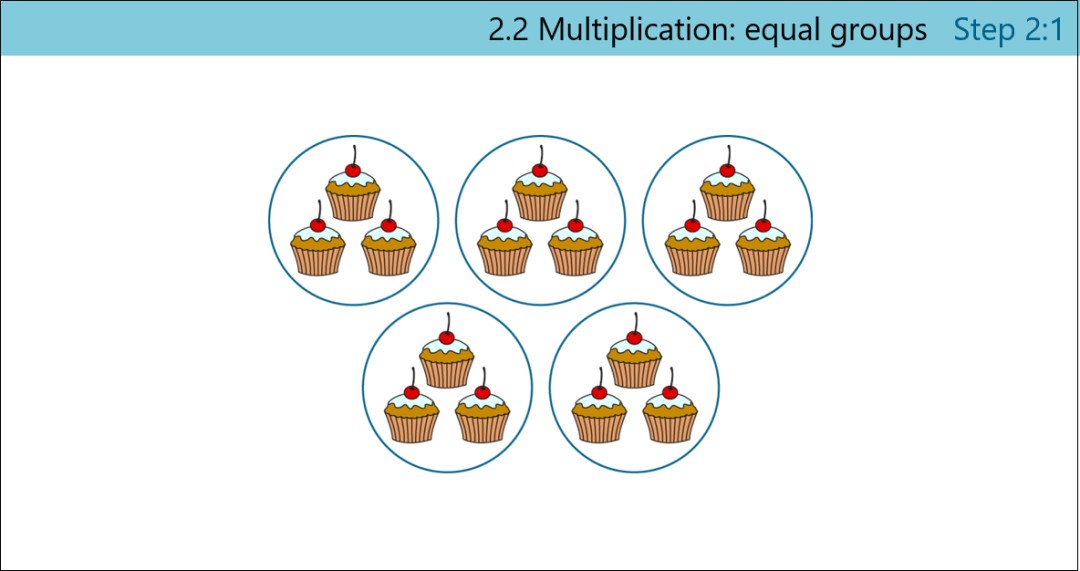
Many slides like this focus on describing the groups – so in this case, there are 5 equal groups and there are 3 cakes in each group. This description requires children to begin to use two units at once: the number of objects in the group, and the number of groups.

Children can still see how to finger-count the cakes, one by one, but they are being gently encouraged to organise the objects into groups (or ‘units’). (Unitising is the focus of Year 1, Unit 9 and you can read more about the concept of unitising in our feature, What is unitising, and why is it important?)

Equal groups as repeated addition

Children start to describe their equal groups using addition expressions. The misconception of confusing the two units (number of objects in the group, and number of groups) is tackled head on:

Equal groups described multiplicatively, alongside repeated addition

Once familiar with building the relevant additive expression, the multiplicative expression is introduced alongside, using the two units that pupils became familiar with in step 1.

Phasing out repeated addition

As children become more familiar with the multiplicative expressions, the additive expressions are phased out:

Note that at this point, children are just understanding how the expression relates to the image, with no focus on the total number of eggs.

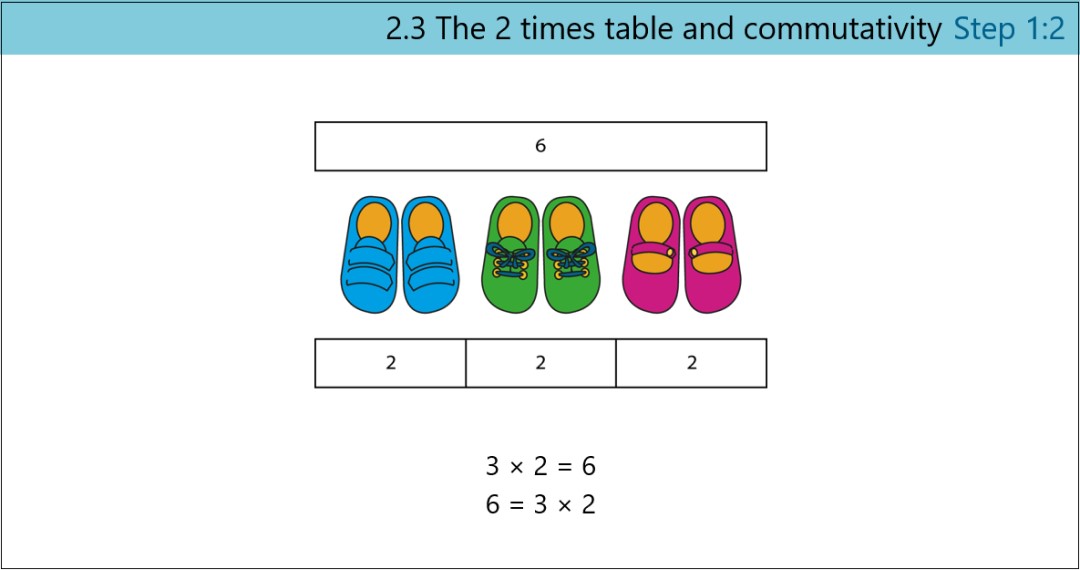
Identifying and explaining each part of the multiplication equation

Only when the expression is fully understood, is it introduced into an equation, with the equals sign and the product. And rather than the equation being introduced as a calculation, it is a further description of the image. With the questions ‘What does the 3 represent?’ ‘What does the 2 represent?’ ‘What does the 6 represent?’ children are encouraged to identify exactly how the equation relates to the image.

All this concept-building comes before any times table learning. When the times table learning begins, later in the unit, with the 2 times table (then 5 and 10), it is built upon strong conceptual understanding with familiar images. So children understand what the times table equations are describing, as well as learning the facts fluently.

A further strengthening of multiplicative concepts comes when children move away from additive thinking completely and understand multiplication as ‘scaling’, where thinking additively will not support them to see the maths. This is addressed in Key Stage 2. The video below shows the animations of a slide designed to demonstrate multiplication as scaling:

This article covers only the introduction of multiplicative thinking – which is further developed throughout primary school, and beyond.

Reference:
Ma, L. and Kessel, C., 2018. The theory of school arithmetic: Whole numbers. In Building the foundation: Whole numbers in the primary grades (pp. 439-463). Springer, Cham.