Multiplying by 10 – is it OK to just put a zero?

In the 2019 autumn term a brief online debate flared up over one small section in our Primary Mastery Professional Development Materials. Some commentators thought that blanket advice was being offered: to teach children ‘to multiply by 10, just put a zero on the end of the number’. This article explains how, under certain conditions, and with secure understanding established, it can be helpful to explore this with pupils.

We all know someone who teaches:

‘to multiply by 10, you just put a zero on the end’.

We were possibly taught that way ourselves. So, what is wrong with that? And in that case, why do the NCETM Primary Mastery Professional Development Materials advocate:

‘to multiply a whole number by 10, place a zero after the final digit of that number’?
(2.13 Calculation: multiplying and dividing by 10 or 100, Step 1.4)

‘It’s all about the development of the concept of multiplying by ten, within a solid framework of understanding place value’, says Liz Lambert, NCETM Assistant Director for Primary.

What’s wrong with ‘just put a zero’?

Being told ‘just put a zero on the end’ (or worse ‘just add a zero’ – there is no adding going on here) pays no attention to whether the child understands what has happened to the place value of the original number – or indeed, whether they understand the concept of place value, or the concept of multiplying. It teaches a trick that will allow the child (if they remember it) to quickly find an answer to:

7 × 10 =

or even:

325,634 × 10 =

But without understanding the underlying concepts, it will remain a trick that can only be used in familiar situations – not the sort of flexible knowledge that can be applied in unfamiliar situations. It can easily lead children, when later multiplying decimals (first addressed in Year 5 – segment 2.19), to conclude:

8.2 × 10 = 8.20

Should we always avoid saying ‘just put a zero’?

So why do the Mastery PD Materials include the phrase:

‘to multiply a whole number by 10, place a zero after the final digit of that number’,

within their Teaching Points for Year 4?

Because by the time children get to this point in Year 4, a number of concepts should have been carefully and sequentially developed:

Year 1:

• Multiples of 10 up to 100 (1.8 Composition of numbers: multiples of 10 up to 100)
• Unitising by counting in units of two, five and ten (2.1 Counting, unitising and coins)

Year 2:

• Connecting multiplication to repeated addition. (2.2 Structures: multiplication representing equal groups)
  (links are to the relevant sections of the NCETM Mastery PD Materials).

In Year 4, children consider the structure of multiplication as scaling rather than just repeated addition, building on prior learning throughout Spine 2 of the materials (Multiplication and Division). Being able to think multiplicatively is a very important conceptual step and one that children often get to secondary school without having mastered. (2.17 Structures: using measures and comparison to understand scaling)

Within this very thorough deep understanding that is developed sequentially through the PD Materials, children are gently encouraged to observe that multiples of ten all end in zero and that indeed an efficient and fluent way to calculate the result of a whole number being multiplied by 10 is to ‘place’ a zero after it. And then, why this works, and the effect of doing it (or not doing it) is discussed in detail.

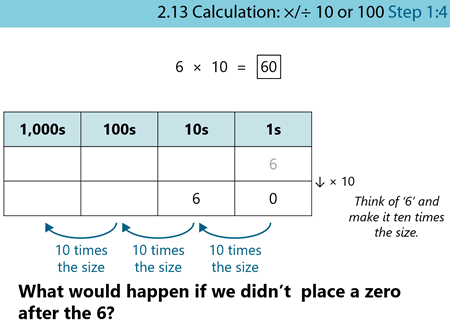
Children need to have secure understanding of the value of the digits in a number. They need to know that 2 is ‘2 ones’ and that 20 is ‘20 ones’ or ‘2 tens’ even without place value column headings.

Children are encouraged to notice that 6 ones becomes 6 tens, or 60 ones.

And here, children are encouraged to notice that 7 ones becomes 7 tens.

Pupils are then encouraged to generalise their result:

The images above are created using representations from Year 4 Teaching Point 2.13 Calculation: multiplying and dividing by 10 or 100.

Within this context of deep conceptual understanding of multiplication and of place value, it would seem bizarre to avoid the observation that you can efficiently multiply whole numbers by 10 by placing a zero, particularly given the importance of this in recognising multiples of 10. So, children are not just told to ‘just place a zero’: the observation of this efficient generalised method is the culmination of lot of conceptual understanding.